Last year I wrote a post about cubicaltt on this blog. Since then there have been a lot of exciting developments in the world of cubes. In particular there are now two cubical proof assistants that are currently being developed in Gothenburg and Pittsburgh. One of them is a cubical version of Agda developed by Andrea Vezzosi at Chalmers and the other is a system called redtt developed by my colleagues at CMU.
These systems differ from cubicaltt in that they are proper proof assistants for cubical type theory in the sense that they support unification, interactive proof development via holes, etc… Cubical Agda inherits Agda’s powerful dependent pattern matching functionality, and redtt has a succinct notation for defining functions by eliminators. Our goal with cubicaltt was never to develop yet another proof assistant, but rather to explore how it could be to program and work in a core system based on cubical type theory. This meant that many things were quite tedious to do in cubicaltt, so it is great that we now have these more advanced systems that are much more pleasant to work in.
This post is about Cubical Agda, but more or less everything in it can also be done (with slight modifications) in redtt. This extension of Agda has actually been around for a few years now, however it is just this year that the theory of HITs has been properly worked out for cubical type theory:
On Higher Inductive Types in Cubical Type Theory
Inspired by this paper (which I will refer as “CHM”) Andrea has extended Cubical Agda with user definable HITs with definitional computation rules for all constructors. Working with these is a lot of fun and I have been doing many of the proofs in synthetic homotopy theory from the HoTT book cubically. Having a system with native support for HITs makes many things a lot easier and most of the proofs I have done are significantly shorter. However, this post will not focus on HITs, but rather on a core library for Cubical Agda that we have been developing over the last few months:
https://github.com/agda/cubical
The core part of this library has been designed with the aim to:
1. Expose and document the cubical primitives of Agda.
2. Provide an interface to HoTT as presented in the book (i.e. “Book HoTT”), but where everything is implemented with the cubical primitives under the hood.
The idea behind the second of these was suggested to me by Martín Escardó who wanted a file which exposes an identity type with the standard introduction principle and eliminator (satisfying the computation rule definitionally), together with function extensionality, univalence and propositional truncation. All of these notions should be represented using cubical primitives under the hood which means that they all compute and that there are no axioms involved. In particular this means that one can import this file in an Agda developments relying on Book HoTT and no axioms should then be needed; more about this later.
Our cubical library compiles with the latest development version of Agda and it is currently divided into 3 main parts:
Cubical.Basics
Cubical.Core
Cubical.HITs
The first of these contain various basic results from HoTT/UF, like isomorphisms are equivalences (i.e. have contractible fibers), Hedberg’s theorem (types with decidable equality are sets), various proofs of different formulations of univalence, etc. This part of the library is currently in flux as I’m adding a lot of results to it all the time.
The second one is the one I will focus on in this post and it is supposed to be quite stable by now. The files in this folder expose the cubical primitives and the cubical interface to HoTT/UF. Ideally a regular user should not have to look too closely at these files and instead just import Cubical.Core.Everything or Cubical.Core.HoTT-UF.
The third folder contains various HITs (S¹, S², S³, torus, suspension, pushouts, interval, join, smash products…) with some basic theory about these. I plan to write another post about this soon, so stay tuned.
As I said above a regular user should only really need to know about the Cubical.Core.Everything and Cubical.Core.HoTT-UF files in the core library. The Cubical.Core.Everything file exports the following things:
-- Basic primitives (some are from Agda.Primitive)
open import Cubical.Core.Primitives public
-- Basic cubical prelude
open import Cubical.Core.Prelude public
-- Definition of equivalences, Glue types and
-- the univalence theorem
open import Cubical.Core.Glue public
-- Propositional truncation defined as a
-- higher inductive type
open import Cubical.Core.PropositionalTruncation public
-- Definition of Identity types and definitions of J,
-- funExt, univalence and propositional truncation
-- using Id instead of Path
open import Cubical.Core.Id public
I will explain the contents of the Cubical.Core.HoTT-UF file in detail later in this post, but I would first like to clarify that it is absolutely not necessary to use that file as a new user. The point of it is mainly to provide a way to make already existing HoTT/UF developments in Agda compute, but I personally only use the cubical primitives provided by the Cubical.Core.Everything file when developing something new in Cubical Agda as I find these much more natural to work with (especially when reasoning about HITs).
Cubical Primitives
It is not my intention to write another detailed explanation of cubical type theory in this post; for that see my previous post and the paper (which is commonly referred to as “CCHM”, after the authors of CCHM):
Cubical Type Theory: a constructive interpretation of the univalence axiom
The main things that the CCHM cubical type theory extends dependent type theory with are:
- An interval pretype
- Kan operations
- Glue types
- Cubical identity types
The first of these is what lets us work directly with higher dimensional cubes in type theory and incorporating this into the judgmental structure is really what makes the system tick. The Cubical.Core.Primitives and Cubical.Core.Prelude files provide 1 and 2, together with some extra stuff that are needed to get 3 and 4 up and running.
Let’s first look at the cubical interval I. It has endpoints i0 : I and i1 : I together with connections and reversals:
_∧_ : I → I → I
_∨_ : I → I → I
~_ : I → I
satisfying the structure of a De Morgan algebra (as in CCHM). As Agda doesn’t have a notion of non-fibrant types (yet?) the interval I lives in Setω.
There are also (dependent) cubical Path types:
PathP : ∀ {ℓ} (A : I → Set ℓ) → A i0 → A i1 → Set ℓ
from which we can define non-dependent Paths:
Path : ∀ {ℓ} (A : Set ℓ) → A → A → Set ℓ
Path A a b = PathP (λ _ → A) a b
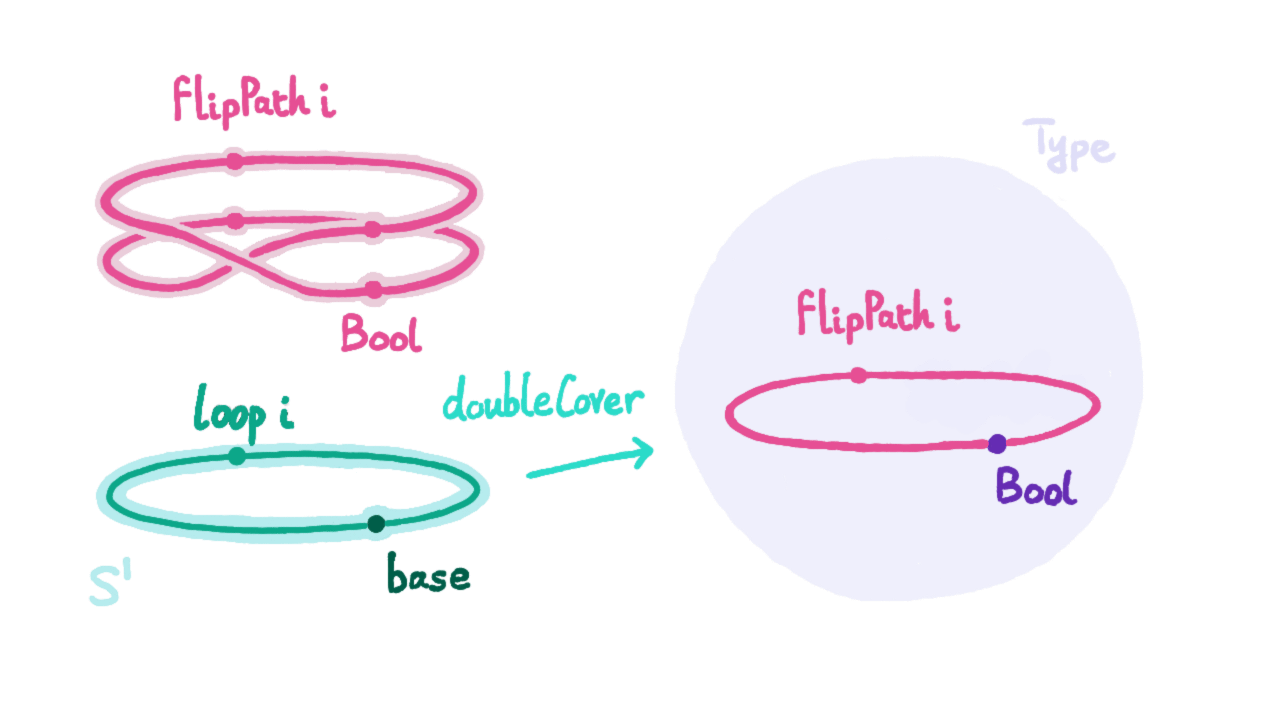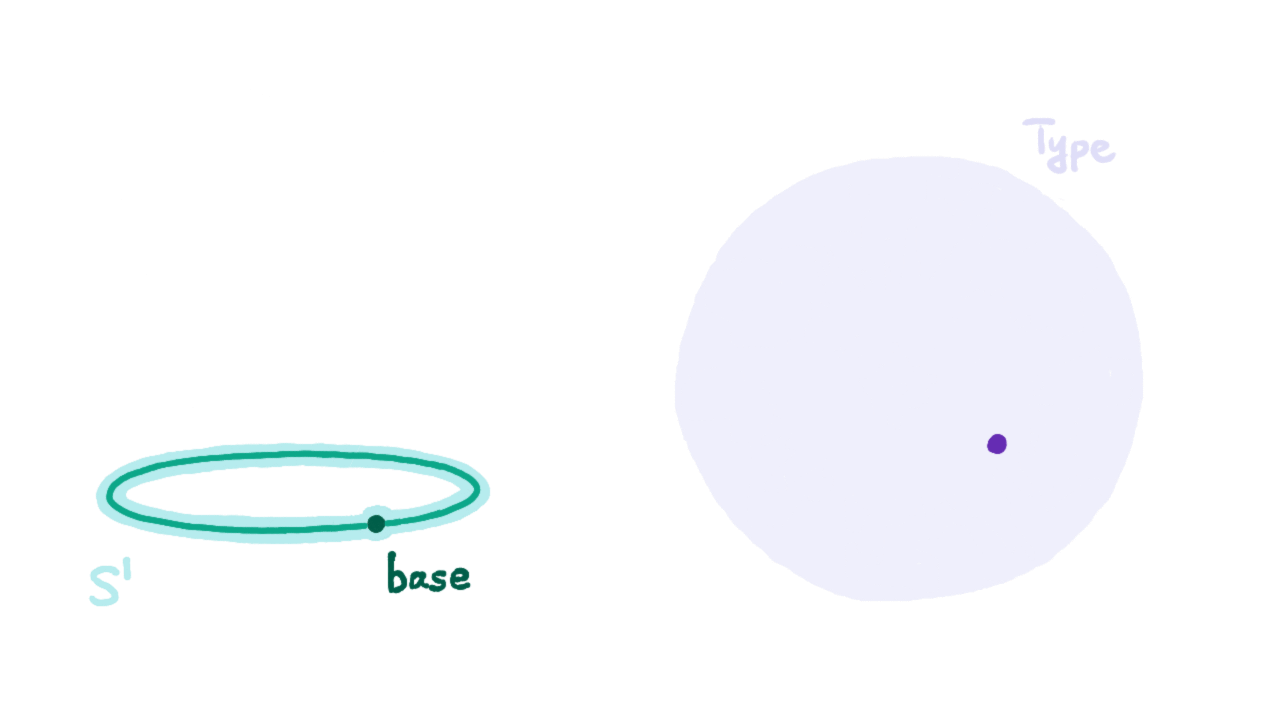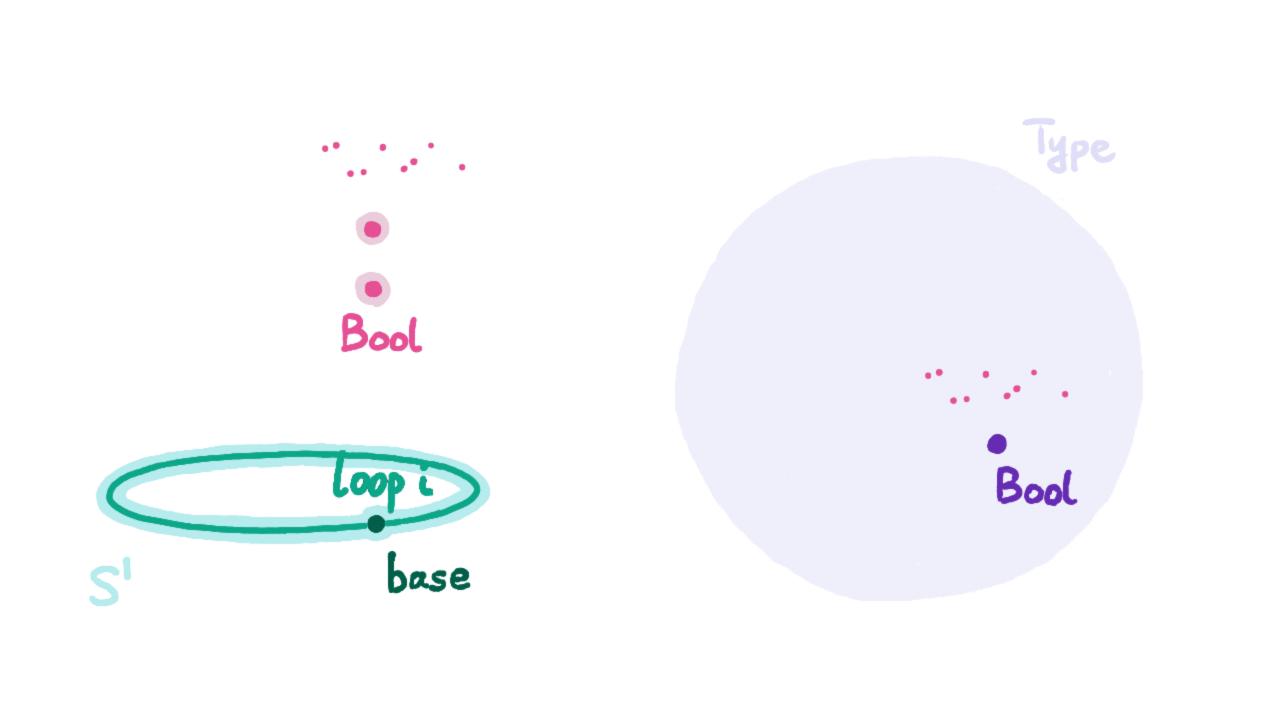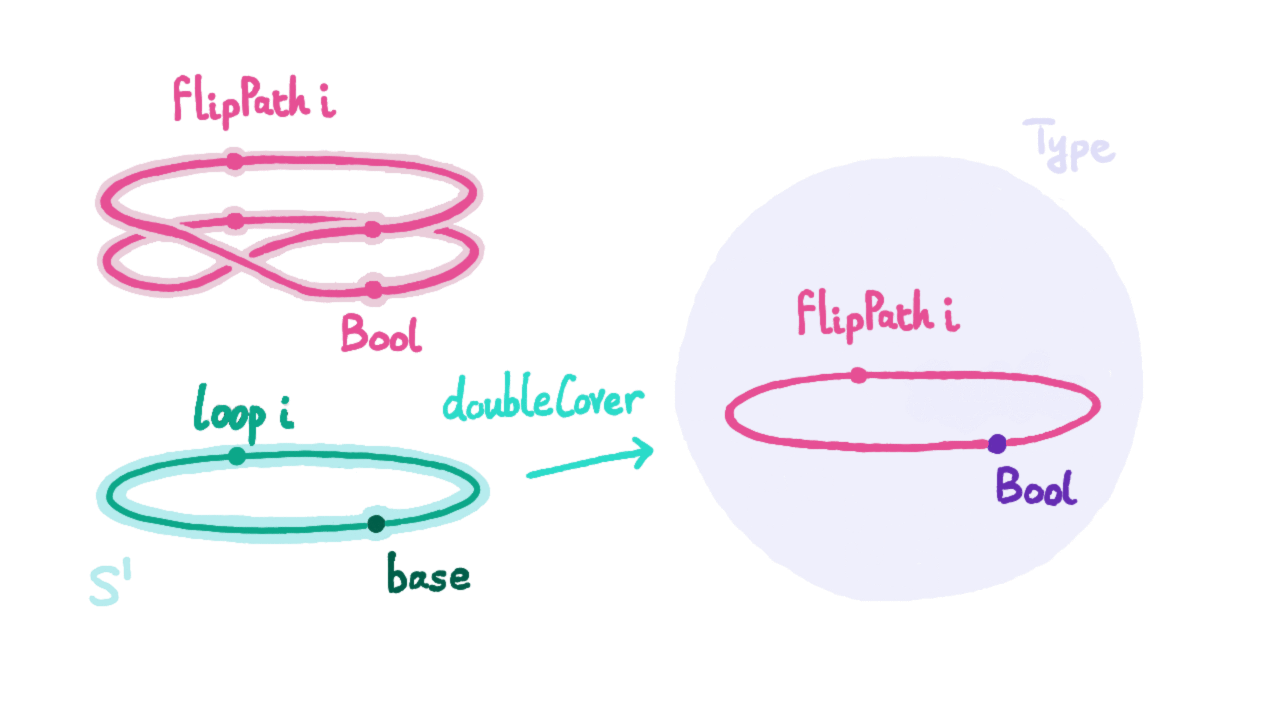
A non-dependent path Path A a b gets printed as a ≡ b. I would like to generalize this at some point and have cubical extension types (inspired by A type theory for synthetic ∞-categories). These extension types are already in redtt and has proved to be very natural and useful, especially for working with HITs as shown by this snippet of redtt code coming from the proof that the loop space of the circle is the integers:
def decode-square
: (n : int)
→ [i j] s1 [
| i=0 → loopn (pred n) j
| i=1 → loopn n j
| j=0 → base
| j=1 → loop i
]
= ...
Just like in cubicaltt we get short proofs of the basic primitives from HoTT/UF:
refl : ∀ {ℓ} {A : Set ℓ} (x : A) → x ≡ x
refl x = λ _ → x
sym : ∀ {ℓ} {A : Set ℓ} {x y : A} → x ≡ y → y ≡ x
sym p = λ i → p (~ i)
cong : ∀ {ℓ ℓ'} {A : Set ℓ} {B : A → Set ℓ'} {x y : A}
(f : (a : A) → B a)
(p : x ≡ y) →
PathP (λ i → B (p i)) (f x) (f y)
cong f p = λ i → f (p i)
funExt : ∀ {ℓ ℓ'} {A : Set ℓ} {B : A → Set ℓ'}
{f g : (x : A) → B x}
(p : (x : A) → f x ≡ g x) →
f ≡ g
funExt p i x = p x i
Note that the proof of functional extensionality is just swapping the arguments to p!
Partial elements and cubical subtypes
[In order for me to be able to explain the other features of Cubical Agda in some detail I have to spend some time on partial elements and cubical subtypes, but as these notions are quite technical I would recommend readers who are not already familiar with them to just skim over this section and read it more carefully later.]
One of the key operations in the cubical set model is to map an element of the interval to an element of the face lattice (i.e. the type of cofibrant propositions F ⊂ Ω). This map is written (_ = 1) : I → F in CCHM and in Cubical Agda it is written IsOne r. The constant 1=1 is a proof that (i1 = 1), i.e. of IsOne i1.
This lets us then work with partial types and elements directly (which was not possible in cubicaltt). The type Partial φ A is a special version of the function space IsOne φ → A with a more extensional judgmental equality. There is also a dependent version PartialP φ A which allows A to be defined only on φ. As these types are not necessarily fibrant they also live in Setω. These types are easiest to understand by seeing how one can introduce them:
sys : ∀ i → Partial (i ∨ ~ i) Set₁
sys i (i = i1) = Set → Set
sys i (i = i0) = Set
This defines a partial type in Set₁ which is defined when (i = i1) ∨ (i = i0). We define it by pattern matching so that it is Set → Set when (i = i1) and Set when (i = i0). Note that we are writing (i ∨ ~ i) and that the IsOne map is implicit. If one instead puts a hole as right hand side:
sys : ∀ i → Partial (i ∨ ~ i) Set₁
sys i x = {! x !}
and ask Agda what the type of x is (by putting the cursor in the hole and typing C-c C-,) then Agda answers:
Goal: Set₁
—————————————————————————————————————————————
x : IsOne (i ∨ ~ i)
i : I
I usually introduce these using pattern matching lambdas so that I can write:
sys' : ∀ i → Partial (i ∨ ~ i) Set₁
sys' i = \ { (i = i0) → Set
; (i = i1) → Set → Set }
This is very convenient when using the Kan operations. Furthermore, when the cases overlap they must of course agree:
sys2 : ∀ i j → Partial (i ∨ (i ∧ j)) Set₁
sys2 i j = \ { (i = i1) → Set
; (i = i1) (j = i1) → Set }
In order to get this to work Andrea had to adapt the pattern-matching of Agda to allow us to pattern-match on the faces like this. It is however not yet possible to use C-c C-c to automatically generate the cases for a partial element, but hopefully this will be added at some point.
Using the partial elements there are also cubical subtypes as in CCHM:
_[_↦_] : ∀ {ℓ} (A : Set ℓ) (φ : I) (u : Partial φ A) →
Agda.Primitive.Setω
A [ φ ↦ u ] = Sub A φ u
So that a : A [ φ ↦ u ] is a partial element a : A that agrees with u on φ. We have maps in and out of the subtypes:
inc : ∀ {ℓ} {A : Set ℓ} {φ} (u : A) →
A [ φ ↦ (λ _ → u) ]
ouc : ∀ {ℓ} {A : Set ℓ} {φ : I} {u : Partial φ A} →
A [ φ ↦ u ] → A
It would be very nice to have subtyping for these, but at the moment the user has to write inc/ouc explicitly. With this infrastructure we can now consider the Kan operations of cubical type theory.
Kan operations
In order to support HITs we use the Kan operations from CHM. The first of these is a generalized transport operation:
transp : ∀ {ℓ} (A : I → Set ℓ) (φ : I) (a : A i0) → A i1
When calling transp A φ a Agda makes sure that A is constant on φ and when calling this with i0 for φ we recover the regular transport function, furthermore when φ is i1 this is the identity function. Being able to control when transport is the identity function is really what makes this operation so useful (see the definition of comp below) and why we got HITs to work so nicely in CHM compared to CCHM.
We also have homogeneous composition operations:
hcomp : ∀ {ℓ} {A : Set ℓ} {φ : I}
(u : I → Partial A φ) (a : A) → A
When calling hcomp A φ u a Agda makes sure that a agrees with u i0 on φ. This is like the composition operations in CCHM, but the type A is constant. Note that this operation is actually different from the one in CHM as φ is in the interval and not the face lattice. By the way the partial elements are set up the faces will then be compared under the image of IsOne. This subtle detail is actually very useful and gives a very neat trick for eliminating empty systems from Cubical Agda (this has not yet been implemented, but it is discussed here).
Using these two operations we can derive the heterogeneous composition
operation:
comp : ∀ {ℓ : I → Level} (A : ∀ i → Set (ℓ i)) {φ : I}
(u : ∀ i → Partial φ (A i))
(u0 : A i0 [ φ ↦ u i0 ]) → A i1
comp A {φ = φ} u u0 =
hcomp
(λ i → λ { (φ = i1) →
transp (λ j → A (i ∨ j)) i (u _ 1=1) })
(transp A i0 (ouc u0))
This decomposition of the Kan operations into transport and homogeneous composition seems crucial to get HITs to work properly in cubical type theory and in fact redtt is also using a similar decomposition of their Kan operations.
We can also derive both homogeneous and heterogeneous Kan filling using hcomp and comp with connections:
hfill : ∀ {ℓ} {A : Set ℓ} {φ : I}
(u : ∀ i → Partial φ A)
(u0 : A [ φ ↦ u i0 ])
(i : I) → A
hfill {φ = φ} u u0 i =
hcomp (λ j → λ { (φ = i1) → u (i ∧ j) 1=1
; (i = i0) → ouc u0 })
(ouc u0)
fill : ∀ {ℓ : I → Level} (A : ∀ i → Set (ℓ i)) {φ : I}
(u : ∀ i → Partial φ (A i))
(u0 : A i0 [ φ ↦ u i0 ])
(i : I) → A i
fill A {φ = φ} u u0 i =
comp (λ j → A (i ∧ j))
(λ j → λ { (φ = i1) → u (i ∧ j) 1=1
; (i = i0) → ouc u0 })
(inc {φ = φ ∨ (~ i)} (ouc {φ = φ} u0))
Using these operations we can do all of the standard cubical stuff, like composing paths and defining J with its computation rule (up to a Path):
compPath : ∀ {ℓ} {A : Set ℓ} {x y z : A} →
x ≡ y → y ≡ z → x ≡ z
compPath {x = x} p q i =
hcomp (λ j → \ { (i = i0) → x
; (i = i1) → q j })
(p i)
module _ {ℓ ℓ'} {A : Set ℓ} {x : A}
(P : ∀ y → x ≡ y → Set ℓ') (d : P x refl) where
J : {y : A} → (p : x ≡ y) → P y p
J p = transp (λ i → P (p i) (λ j → p (i ∧ j))) i0 d
JRefl : J refl ≡ d
JRefl i = transp (λ _ → P x refl) i d
The use of a module here is not crucial in any way, it’s just an Agda trick to make J and JRefl share some arguments.
Glue types and univalence
The file Cubical.Core.Glue defines fibers and equivalences (as they were originally defined by Voevodsky in his Foundations library, i.e. as maps with contractible fibers). Using this we export the Glue types of Cubical Agda which lets us extend a total type by a partial family of equivalent types:
Glue : ∀ {ℓ ℓ'} (A : Set ℓ) {φ : I} →
(Te : Partial φ (Σ[ T ∈ Set ℓ' ] T ≃ A)) →
Set ℓ'
This comes with introduction and elimination forms (glue and unglue). With this we formalize the proof of a variation of univalence following the proof in Section 7.2 of CCHM. The key observation is that unglue is an equivalence:
unglueIsEquiv : ∀ {ℓ} (A : Set ℓ) (φ : I)
(f : PartialP φ (λ o → Σ[ T ∈ Set ℓ ] T ≃ A)) →
isEquiv {A = Glue A f} (unglue {φ = φ})
equiv-proof (unglueIsEquiv A φ f) = λ (b : A) →
let u : I → Partial φ A
u i = λ{ (φ = i1) → equivCtr (f 1=1 .snd) b .snd (~ i) }
ctr : fiber (unglue {φ = φ}) b
ctr = ( glue (λ { (φ = i1) → equivCtr (f 1=1 .snd) b .fst }) (hcomp u b)
, λ j → hfill u (inc b) (~ j))
in ( ctr
, λ (v : fiber (unglue {φ = φ}) b) i →
let u' : I → Partial (φ ∨ ~ i ∨ i) A
u' j = λ { (φ = i1) → equivCtrPath (f 1=1 .snd) b v i .snd (~ j)
; (i = i0) → hfill u (inc b) j
; (i = i1) → v .snd (~ j) }
in ( glue (λ { (φ = i1) → equivCtrPath (f 1=1 .snd) b v i .fst }) (hcomp u' b)
, λ j → hfill u' (inc b) (~ j)))
The details of this proof is best studied interactively in Agda and by first understanding the proof in CCHM. The reason this is a crucial observation is that it says that any partial family of equivalences can be extended to a total one from Glue [ φ ↦ (T,f) ] A to A:
unglueEquiv : ∀ {ℓ} (A : Set ℓ) (φ : I)
(f : PartialP φ (λ o → Σ[ T ∈ Set ℓ ] T ≃ A)) →
(Glue A f) ≃ A
unglueEquiv A φ f = ( unglue {φ = φ} , unglueIsEquiv A φ f )
and this is exactly what we need to prove the following formulation of the univalence theorem:
EquivContr : ∀ {ℓ} (A : Set ℓ) → isContr (Σ[ T ∈ Set ℓ ] T ≃ A)
EquivContr {ℓ} A =
( ( A , idEquiv A)
, λ w i →
let f : PartialP (~ i ∨ i) (λ x → Σ[ T ∈ Set ℓ ] T ≃ A)
f = λ { (i = i0) → ( A , idEquiv A ) ; (i = i1) → w }
in ( Glue A f , unglueEquiv A (~ i ∨ i) f) )
This formulation of univalence was proposed by Martín Escardó in (see also Theorem 5.8.4 of the HoTT Book):
https://groups.google.com/forum/#!msg/homotopytypetheory/HfCB_b-PNEU/Ibb48LvUMeUJ
We have also formalized a quite slick proof of the standard formulation of univalence from EquivContr (see Cubical.Basics.Univalence). This proof uses that EquivContr is contractibility of singletons for equivalences, which combined with subst can be used to prove equivalence induction:
contrSinglEquiv : ∀ {ℓ} {A B : Set ℓ} (e : A ≃ B) →
(B , idEquiv B) ≡ (A , e)
contrSinglEquiv {A = A} {B = B} e =
isContr→isProp (EquivContr B) (B , idEquiv B) (A , e)
EquivJ : ∀ {ℓ ℓ′} (P : (A B : Set ℓ) → (e : B ≃ A) → Set ℓ′)
(r : (A : Set ℓ) → P A A (idEquiv A))
(A B : Set ℓ) (e : B ≃ A) →
P A B e
EquivJ P r A B e =
subst (λ x → P A (x .fst) (x .snd))
(contrSinglEquiv e) (r A)
We then use that the Glue types also gives a map ua which maps the identity equivalence to refl:
ua : ∀ {ℓ} {A B : Set ℓ} → A ≃ B → A ≡ B
ua {A = A} {B = B} e i =
Glue B (λ { (i = i0) → (A , e)
; (i = i1) → (B , idEquiv B) })
uaIdEquiv : ∀ {ℓ} {A : Set ℓ} → ua (idEquiv A) ≡ refl
uaIdEquiv {A = A} i j =
Glue A {φ = i ∨ ~ j ∨ j} (λ _ → A , idEquiv A)
Now, given any function au : ∀ {ℓ} {A B : Set ℓ} → A ≡ B → A ≃ B satisfying auid : ∀ {ℓ} {A B : Set ℓ} → au refl ≡ idEquiv A we directly get that this is an equivalence using the fact that any isomorphism is an equivalence:
module Univalence
(au : ∀ {ℓ} {A B : Set ℓ} → A ≡ B → A ≃ B)
(auid : ∀ {ℓ} {A B : Set ℓ} → au refl ≡ idEquiv A) where
thm : ∀ {ℓ} {A B : Set ℓ} → isEquiv au
thm {A = A} {B = B} =
isoToIsEquiv {B = A ≃ B} au ua
(EquivJ (λ _ _ e → au (ua e) ≡ e)
(λ X → compPath (cong au uaIdEquiv)
(auid {B = B})) _ _)
(J (λ X p → ua (au p) ≡ p)
(compPath (cong ua (auid {B = B})) uaIdEquiv))
We can then instantiate this with for example the au map defined using J (which is how Vladimir originally stated the univalence axiom):
eqweqmap : ∀ {ℓ} {A B : Set ℓ} → A ≡ B → A ≃ B
eqweqmap {A = A} e = J (λ X _ → A ≃ X) (idEquiv A) e
eqweqmapid : ∀ {ℓ} {A : Set ℓ} → eqweqmap refl ≡ idEquiv A
eqweqmapid {A = A} = JRefl (λ X _ → A ≃ X) (idEquiv A)
univalenceStatement : ∀ {ℓ} {A B : Set ℓ} →
isEquiv (eqweqmap {ℓ} {A} {B})
univalenceStatement = Univalence.thm eqweqmap eqweqmapid
Note that eqweqmapid is not proved by refl, instead we need to use the fact that the computation rule for J holds up to a Path. Furthermore, I would like to emphasize that there is no problem with using J for Path’s and that the fact that the computation rule doesn’t hold definitionally is almost never a problem for practical formalization as one rarely use it as it is often more natural to just use the cubical primitives. However, in Section 9.1 of CCHM we solve this by defining cubical identity types satisfying the computation rule definitionally (following a trick of Andrew Swan).
Cubical identity types
The idea behind the cubical identity types is that an element of an identity type is a pair of a path and a formula which tells us where this path is constant, so for example reflexivity is just the constant path together with the fact that it is constant everywhere (note that the interval variable comes before the path as the path depends on it):
refl : ∀ {ℓ} {A : Set ℓ} {x : A} → Id x x
refl {x = x} = ⟨ i1 , (λ _ → x) ⟩
These types also come with an eliminator from which we can prove J such that it is the identity function on refl, i.e. where the computation rule holds definitionally (for details see the Agda code in Cubical.Core.Id). We then prove that Path and Id are equivalent types and develop the theory that we have for Path for Id as well, in particular we prove the univalence theorem expressed with Id everywhere (the usual formulation can be found in Cubical.Basics.UnivalenceId).
Note that the cubical identity types are not an inductive family like in HoTT which means that we cannot use Agda’s pattern-matching to match on them. Furthermore Cubical Agda doesn’t support inductive families yet, but it should be possible to adapt the techniques of Cavallo/Harper presented in
Higher Inductive Types in Cubical Computational Type Theory
in order to extend it with inductive families. The traditional identity types could then be defined as in HoTT and pattern-matching should work as expected.
Propositional truncation
The core library only contains one HIT: propositional truncation (Cubical.Core.PropositionalTruncation). As Cubical Agda has native support for user defined HITs this is very convenient to define:
data ∥_∥ {ℓ} (A : Set ℓ) : Set ℓ where
∣_∣ : A → ∥ A ∥
squash : ∀ (x y : ∥ A ∥) → x ≡ y
We can then prove the recursor (and eliminator) using pattern-matching:
recPropTrunc : ∀ {ℓ} {A : Set ℓ} {P : Set ℓ} →
isProp P → (A → P) → ∥ A ∥ → P
recPropTrunc Pprop f ∣ x ∣ = f x
recPropTrunc Pprop f (squash x y i) =
Pprop (recPropTrunc Pprop f x) (recPropTrunc Pprop f y) i
However I would not only use recPropTrunc explicitly as we can just use pattern-matching to define functions out of HITs. Note that the cubical machinery makes it possible for us to define these pattern-matching equations in a very nice way without any ap‘s. This is one of the main reasons why I find it a lot more natural to work with HITs in cubical type theory than in Book HoTT: the higher constructors of HITs construct actual elements of the HIT, not of its identity type!
This is just a short example of what can be done with HITs in Cubical Agda, I plan to write more about this in a future post, but for now one can look at the folder Cubical/HITs for many more examples (S¹, S², S³, torus, suspension, pushouts, interval, join, smash products…).
Constructive HoTT/UF
By combining everything I have said so far we have written the file Cubical.Core.HoTT-UF which exports the primitives of HoTT/UF defined using cubical machinery under the hood:
open import Cubical.Core.Id public
using ( _≡_ -- The identity type.
; refl -- Unfortunately, pattern matching on refl is not available.
; J -- Until it is, you have to use the induction principle J.
; transport -- As in the HoTT Book.
; ap
; _∙_
; _⁻¹
; _≡⟨_⟩_ -- Standard equational reasoning.
; _∎
; funExt -- Function extensionality
-- (can also be derived from univalence).
; Σ -- Sum type. Needed to define contractible types, equivalences
; _,_ -- and univalence.
; pr₁ -- The eta rule is available.
; pr₂
; isProp -- The usual notions of proposition, contractible type, set.
; isContr
; isSet
; isEquiv -- A map with contractible fibers
-- (Voevodsky's version of the notion).
; _≃_ -- The type of equivalences between two given types.
; EquivContr -- A formulation of univalence.
; ∥_∥ -- Propositional truncation.
; ∣_∣ -- Map into the propositional truncation.
; ∥∥-isProp -- A truncated type is a proposition.
; ∥∥-recursion -- Non-dependent elimination.
; ∥∥-induction -- Dependent elimination.
)
The idea is that if someone has some code written using HoTT/UF axioms in Agda they can just import this file and everything should compute properly. The only downside is that one has to rewrite all pattern-matches on Id to explicit uses of J, but if someone is willing to do this and have some cool examples that now compute please let me know!
That’s all I had to say about the library for now. Pull-requests and feedback on how to improve it are very welcome! Please use the Github page for the library for comments and issues:
https://github.com/agda/cubical/issues
If you find some bugs in Cubical Agda you can use the Github page of Agda to report them (just check that no-one has already reported the bug):
https://github.com/agda/agda/issues










 (♣)
(♣)
![$$\xymatrix{ \sum\limits_{x:2} Q(i(x)) \pullbackarrow[ddr] \ar[r] \ar[dd]^-{\texttt{pr}_1} & \sum\limits_{x : I} Q(x) \ar[dd]^-{\texttt{pr}_1} \\ \\ 2 \ar@/^/[uu]^-{\texttt{myst\_pi\_i}} \ar[r]_i & I \ar@/^/[uu]^-{\texttt{myst\_sig}} }$$](https://hottheory.files.wordpress.com/2014/02/myst_pi_fibration_diagram.png?h=175)
![$$\xymatrix{ B \ar[rr]_-g && \sum\limits_{x:B} Q(x)\ar@/_/[ll]_-{\texttt{pr}_1} \\ A \ar[rr]_-f && B \\ A \ar[rr]_-{\text{``$g\circ f$''}} && \sum\limits_{x:A}Q(f(x)) \ar@/_/[ll]_-{\texttt{pr}_1} \ar[rr] && \sum\limits_{y:B} Q(y) }$$](https://hottheory.files.wordpress.com/2014/02/composition_diagram.png?h=200)
![$$\xymatrix{ \text{sections of fibrations} \ar@{^{(}->}[d] \ar@{}[drr]|-{\text{\color{red}\huge\xmark}} && \text{functions}\ar[ll] \ar@{}[d]|{\rotatebox{90}{$\subseteq$}} \\ \text{morphisms of types} \ar@/^/[rr] \ar@{}[rr]|-{\cong} && \text{non-dependent functions} \ar@/^/[ll] }$$](https://hottheory.files.wordpress.com/2014/02/no_commute.png?h=95)