Homotopy Type Theory and Univalent Foundations

This site serves to collect and disseminate research, resources, and tools for the investigation of homotopy type theory, and hosts a blog for those involved in its study.

Homotopy Type Theory refers to a new field of study relating Martin-Löf’s system of intensional, constructive type theory with abstract homotopy theory.  Propositional equality is interpreted as homotopy and type isomorphism as homotopy equivalence. Logical constructions in type theory then correspond to homotopy-invariant constructions on spaces, while theorems and even proofs in the logical system inherit a homotopical meaning.  As the natural logic of homotopy, constructive type theory is also related to higher category theory as it is used e.g. in the notion of a higher topos.

Univalent Foundations of Mathematics is Vladimir Voevodsky’s new program for a comprehensive, computational foundation for mathematics based on the homotopical interpretation of type theory. The type theoretic univalence axiom relates propositional equality on the universe with homotopy equivalence of small types. The program is currently being implemented with the help of the automated proof assistant Coq.  The Univalent Foundations program is closely tied to homotopy type theory and is being pursued in parallel by many of the same researchers.

1 Response to Homotopy Type Theory and Univalent Foundations

  1. HoTT says:
    20 March 2011 at 11:23

    Here is a page that explains how to use LaTeX in a WordPress posting. Basically, instead of writing $formula$ you write “latex formula” enclosed in $-signs. It even works in comments: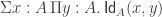 \Sigma x:A\, \Pi y:A.\, \mathsf{Id}_A(x,y).

Comments are closed.