As some of you might remember, back in 2015 at the meeting of the german mathematical society in Hamburg, Urs Schreiber presented three problems or “exercises” as he called it back then. There is a page about that on the nLab, if you want to know more. In this post, I will sketch a solution to some part of the first of these problems, while the occasion of writing it is a new version of my article about this, which now comes with a long introduction.
Urs Schreiber’s problems were all about formalizing results in higher differential geometry, that make also sense in the quite abstract setting of differential cohesive toposes and cohesive toposes.
A differential cohesive topos is a topos with some extra structure given by three monads and three comonads with some nice properties and adjunctions between them. There is some work concerned with having this structure in homotopy type theory. A specialized cohesive homotopy type theory concerned with three of the six (co-)monads, called real-cohesive homotopy type theory was introduced by Mike Shulman.
What I want to sketch here today is concerned only with one of the monads of differential cohesion. I will call this monad coreduction and denote it with . By the axioms of differential cohesion, it has a left and a right adjoint and is idempotent. These properties are more than enough to model a monadic modality in homotopy type theory. Monadic modalities were already defined at the end of section 7 in the HoTT-Book and named just “modalities” and it is possible to have a homotopy type theory with a monadic modality just by adding some axioms — which is known not to work for non-trivial comonadic modalities.
So let us assume that is a monadic modality in HoTT. That means that we have a map
and a unit
such that a property holds, that I won’t really go into in this post — but here it is for completeness: For any dependent type on some type
, such that the unit maps
are equivalences for all
, the map
is an equivalence. So the inverse to this map is an induction principle, that only holds for dependent types subject to the condition above.
The n-truncations and double negation are examples of monadic modalities.
At this point (or earlier), one might ask: “Where is the differential geometry”? The answer is that in this setting, all types carry differential geometric structure that is accessible via and
. This makes sense if we think of some very special interpretations of
and
(and HoTT), where the unit
is given as the quotient map from a space
to its quotient
by a relation that identifies infinitesimally close points in
.
Since we have this abstract monadic modality, we can turn this around and define the notion of two points being infinitesimally close, denoted “
” in terms of the units:
where “” denotes the identity type (of
in this case). The collection of all points y in a type X that are infinitesimally close to a fixed x in X, is called the formal disk at x. Let us denote it with
:
Using some basic properties of monadic modalities, one can show, that any map preserves inifinitesimal closeness, i.e.
is inhabited. For any x in A, we can use this to get a map
which behaves a lot like the differential of a smooth function. For example, the chain rule holds
and if f is an equivalence, all induced are also equivalences. The latter corresponds to the fact that the differential of a diffeomorphism is invertible.
If we have a 0-group G with unit e, the left tranlations are a family of equivalences that consistently identify
with all other formal disks
in G given by the differentials
.
This is essentially a generalization of the fact, that the tangent bundle of a Lie-group is trivialized by left translations and a solution to the first part of the first of Urs Schreiber’s problems I mentioned in the beginning.
With the exception of the chain rule, all of this was in my dissertation, which I defended in 2017. A couple of month ago, I wrote an article about this and put it on the arxiv and since monday, there is an improved version with an introduction that explains what monads you can think of and relates the setup to Synthetic Differential Geometry.
There is also a recording on youtube of a talk I gave about this in Bonn.
Could your results work for a modality corresponding to germs rather than jets? Borisov and Kreminzer are looking to contract at infinity-nilpotent neighbourhoods: https://nforum.ncatlab.org/discussion/2523/jet-bundle/?Focus=66961#Comment_66961
Thanks for pointing out the work of Borisov and Kreminzer! I wasn’t aware of it.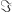 is defined by precomposition with reduction and its properties can be derived from the fact that reduction is a coreflection (on affine schemes).
is defined by precomposition with reduction and its properties can be derived from the fact that reduction is a coreflection (on affine schemes). on
on 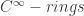 and if I guess correctly how they move on, we get a different version of the de Rham space by precomposing presheaves with that coreflection.
and if I guess correctly how they move on, we get a different version of the de Rham space by precomposing presheaves with that coreflection.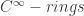 , you can get a monad
, you can get a monad 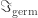 that has the same nice abstract properties that
that has the same nice abstract properties that 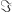 has.
has.
Short answer: The results work for any (monadic) modality and this seems to be one – at least on presheaves.
On presheaves
According to Borisov and Kreminzer, there is a coreflection
So if we just look at presheaves on
Is there a problem with making it work for sheaves too?
It can happen that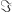 (=precomposition with the usual reduction) does not preserve sheaves. I’m afraid I don’t have a counterexample. On affine schemes with the usual reduction, it is enough to see that covers are preserved by reduction and reduced objects are always covered by reduced objects to show that
(=precomposition with the usual reduction) does not preserve sheaves. I’m afraid I don’t have a counterexample. On affine schemes with the usual reduction, it is enough to see that covers are preserved by reduction and reduced objects are always covered by reduced objects to show that 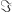 preserves sheaves. That is true for the Zariski topology and the étale topology. For the Zariski topology (which should be more interesting here), this follows from the algebraic fact, that localizing commutes with reduction. So a possible attempt for a proof would be to show a similar property for the topology on
preserves sheaves. That is true for the Zariski topology and the étale topology. For the Zariski topology (which should be more interesting here), this follows from the algebraic fact, that localizing commutes with reduction. So a possible attempt for a proof would be to show a similar property for the topology on 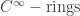 .
. , which I never really thought about. Maybe checking that the result is still modal for
, which I never really thought about. Maybe checking that the result is still modal for  leads to the similar conditions as above.
leads to the similar conditions as above. is called “de Rham prestack” in contexts where finer topologies are used.
is called “de Rham prestack” in contexts where finer topologies are used.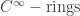 to know if this is ok), i.e. come from localizations maps of the form
to know if this is ok), i.e. come from localizations maps of the form ![R \to R[f^{-1}]](https://s0.wp.com/latex.php?latex=R+%5Cto+R%5Bf%5E%7B-1%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Then modding out
. Then modding out  -nilpotents is (like with reduction) just modding out an ideal, so it commutes with this localization.
-nilpotents is (like with reduction) just modding out an ideal, so it commutes with this localization.
Another approach would be to sheafify after applying
A hint that just sheafifying doesn’t help in general is that
So my first guess is, that it also works for sheaves. An argument could go like this:
Without loss of generality a cover consists of subsets that are the non-zeros of a function (don’t know enough about
For what it’s worth, the germ of the diagonal idea led to the concept of (tangent) microbundle, as Jim Stasheff remarks https://golem.ph.utexas.edu/category/2007/08/more_on_tangent_categories.html#c011887.
Just to remind us that a germ-scale shape modality should be related to Bunge et al.’s “Synthetic Differential Topology”. I once made a brief note on this in the nLab entry of that title (lower case). But check.
Here is the link to this nLab-page: -reduction on
-reduction on 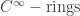 . As I understand it, it behaves more like reduction in Algebraic Geometry than the actual reduction on
. As I understand it, it behaves more like reduction in Algebraic Geometry than the actual reduction on 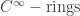 . At least with respect to all the properties of reduction I use in the algebraic world, to show that
. At least with respect to all the properties of reduction I use in the algebraic world, to show that 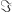 preserves sheaves. So now, I convinced myself that
preserves sheaves. So now, I convinced myself that 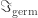 (induced by
(induced by  -reduction) is a modality, but realized that I don’t really know why
-reduction) is a modality, but realized that I don’t really know why  (induced by the usual reduction) should be a modality (on
(induced by the usual reduction) should be a modality (on  ).
).
synthetic differential topology
I looked more closely at the
One neat feature of this differentially-cohesive synthetic formulation of V-manifolds is that, due to the ambient homotopy theory, the resulting V-manifolds are in general not plain manifolds, but are orbifolds, in fact may be infinity-orbifolds, usually known as “etale infinity-stacks” (Prop. 6.5.60 in dcct).
In order to reduce this freedom, we may pick a group object G_glob and ask that a given V-manifold X admits a faithful (i.e. 0-truncated) map to B G_glob. This condition ensures that the isotropy groups of X are subgroups of G_glob. If, in the standard model, G_glob is a compact Lie group, this means that X is then constrained to be an orbifold which admits local charts of the form U_i//G_i, where G_i is any discrete subgroup of G_glob (with some 0-type U_i).
We may then consider any other type A equipped with a faithful (0-truncated) map to BG_glob, and consider the function type
H(X,A) := X –> A
in the slice over BG_glob (i.e. as a map of dependent types in context BG_glob). I think this is equivalently the “global equivariant” orbifold cohomology of X with coefficients in the “global space” A, for the underlying family of equivariance groups being that of finite subgroups of G_glob.
I have tried to spell out this last staement at nLab:orbifold cohomology.
This should be pretty interesting.