Specific violations of parametricity, or existence of non-identity automorphisms of the universe, can be used to prove classical axioms. The former was previously featured on this blog, and the latter is part of a discussion on the HoTT mailing list. In a cooperation between Martín Escardó, Peter Lumsdaine, Mike Shulman, and myself, we have strengthened these results and recorded them in a paper that is now on arXiv.
In this blog post, we work with the full repertoire of HoTT axioms, including univalence, propositional truncations, and pushouts. For the paper, we have carefully analysed which assumptions are used in which theorem, if any.
Parametricity
Parametricity is a property of terms of a language. If your language only has parametric terms, then polymorphic functions have to be invariant under the type parameter. So in MLTT, the only term inhabiting the type of polymorphic endomaps is the polymorphic identity
.
In univalent foundations, we cannot prove internally that every term is parametric. This is because excluded middle is not parametric (exercise 6.9 of the HoTT book tells us that, assuming LEM, we can define a polymorphic endomap that flips the booleans), but there exist classical models of univalent foundations. So if we could prove this internally, excluded middle would be false, and thus the classical models would be invalid.
In the abovementioned blog post, we observed that exercise 6.9 of the HoTT book has a converse: if is the flip map on the type of booleans, then excluded middle holds. In the paper on arXiv, we have a stronger result:
Theorem. There exist and a type
and a point
with
if and only if excluded middle holds.
Notice that there are no requirements on the type or the point
. We have also applied the technique used for this theorem in other scenarios, for example:
Theorem. There exist and types
and points
with
if and only if weak excluded middle holds.
The results in the paper illustrate that different violations of parametricity have different proof-theoretic strength: some violations are impossible, while others imply varying amounts of excluded middle.
Automorphisms of the universe
In contrast to parametricity, which proves that terms of some language necessarily have some properties, it is currently unknown if non-identity automorphisms of the universe are definable in univalent foundations. But some believe that this may not be the case.
In the presence of excluded middle, we can define non-identity automorphisms of the universe. Given a type , we use excluded middle to decide if
is a proposition. If it is, we map
to
, and otherwise we map
to itself. Assuming excluded middle, we have
for any proposition, so this is an automorphism.
The above automorphism swaps the empty type with the unit type
and leaves all other types unchanged. More generally, assuming excluded middle we can swap any two types with equivalent automorphism ∞-groups, since in that case the corresponding connected components of the universe are equivalent. Still more generally, we can permute arbitrarily any family of types all having the same automorphism ∞-group.
The simplest case of this is when all the types are rigid, i.e. have trivial automorphism ∞-group. The types and
are both rigid, and at least with excluded middle no other sets are; but there can be rigid higher types. For instance, if
is a group that is a set (i.e. a 1-group), then its Eilenberg-Mac Lane space
is a 1-type, and its automorphism ∞-group is a 1-type whose
is the outer automorphisms of
and whose
is the center of
. Thus, if
has trivial outer automorphism group and trivial center, then
is rigid. Such groups are not uncommon, including for instance the symmetric group
for any
. Thus, assuming excluded middle we can permute these
arbitrarily, producing uncountably many automorphisms of the universe.
In the converse direction, we recorded the following.
Theorem. If there is an automorphism of the universe that maps some inhabited type to the empty type, then excluded middle holds.
Corollary. If there is an automorphism of the universe with
, then the double negation
of the law of excluded middle holds.
This corollary relates to an unclaimed prize: if from an arbitrary equivalence such that
for a particular
you get a non-provable consequence of excluded middle, then you get
-many beers. So this corollary wins you 0 beers. Although perhaps sober, we think this is an achievement worth recording.
Using this corollary, in turn, we can win -many beers, where
is excluded middle for propositions in the universe
. If
we have
. Suppose
is an automorphism of
with
, then
. For suppose that
, and hence
. So by the corollary, we obtain
. But
implies
by cumulativity, so
also holds, contradicting our assumption that
.
To date no one has been able to win 1 beer.
It’s a nice paper! Here’s a tiny positive observation regarding automorphisms of the universe: if we have an equivalence together with
together with  , then
, then 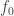 is the identity. Indeed, plugging
is the identity. Indeed, plugging  and
and  into
into 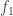 , we get
, we get 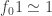 , and then plugging
, and then plugging  and an arbitrary
and an arbitrary  , we get
, we get  . Presumably, having more and more components of an automorphism of the universe as an
. Presumably, having more and more components of an automorphism of the universe as an  -category, will entail that more and more of these components are those of the identity automorphism. So the first question is: how much do we need to add to ensure that also
-category, will entail that more and more of these components are those of the identity automorphism. So the first question is: how much do we need to add to ensure that also 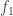 is the identity?
is the identity?
Egbert’s recent arxiv post about the join construction, in which he shows that the propositions are precisely the “canonical” idempotents for the join, now has me wondering: how many idempotents are there on the universe?
Of course, any constant function is idempotent, as is the identity. And if P is any proposition, then and
and  are both idempotent. If
are both idempotent. If  , then the former is constant at 0 and the latter is the identity; while if
, then the former is constant at 0 and the latter is the identity; while if  , then the former is the identity and the latter is constant at 1. Of course, with excluded middle we can construct other idempotents, like sending X to 0 if it is empty and to 1 if it is inhabited. Can we construct any nonidentity, nonconstant idempotents on the universe without using classical axioms? Can we derive a taboo from the assumption of a nonidentity, nonconstant idempotent on the universe?
, then the former is the identity and the latter is constant at 1. Of course, with excluded middle we can construct other idempotents, like sending X to 0 if it is empty and to 1 if it is inhabited. Can we construct any nonidentity, nonconstant idempotents on the universe without using classical axioms? Can we derive a taboo from the assumption of a nonidentity, nonconstant idempotent on the universe?
Consider any type with an identity
with an identity  , such as the natural numbers. Then
, such as the natural numbers. Then  and
and 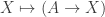 are examples of non-identity, non-constant idempotents. In the case when
are examples of non-identity, non-constant idempotents. In the case when  is the natural numbers, we also have the example
is the natural numbers, we also have the example  as we have an identity
as we have an identity 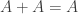 as well.
as well.
You must have had something else in mind. Another class of examples are n-truncations. In a similar vein, the double negation of a type is an idempotent.
But I have a similar question: can we define a non-trivial embedding of the universe into itself without using (a consequence of) excluded middle?
That’s a very kind way of saying “your brain must have been turned off”. (-:O
I am sure I have said things in the internet with my brain switched off, too. And I am sure I have said silly things with my brain switched on, in the internet and otherwise. 🙂