Can the type of truth values be given the structure of a group?

When attempting to prove a theorem, not discussed in this post, I tried to give a certain set the structure of a group. After failing repeatedly, my proof attempts led me to consider a miniature version of the problem: can $\Omega$ , the object of truth values, be given the structure of a group?

This question makes sense in 1-topos theory, in $\infty$ -topos theory and in HoTT/UF, where in the latter a truth value is a type with at most one element, also known as a proposition (and sometimes as an h-proposition or as a mere proposition).

The answer to the question, in all cases, turns out to be that $\Omega$ can be given the structure of a group if and only if the topos is boolean.

Reasoning in the internal language, or the type theory, the argument is as follows.

If the topos is boolean, that is, excluded middle holds in the internal language, then trivially $\Omega$ has precisely two group structures, and $\Omega$ endowed with each of them gives rise to two isomorphic groups.

It is the converse that is interesting.

We use “Higgs’ Involution Theorem”, which says that every left-cancellable map $f : \Omega \to \Omega$ is an involution, that is, $f (f p) = p$ .

If a group structure $(\oplus , 0)$ on $\Omega$ is given, by Higgs’ involution
theorem we conclude that it is abelian with $p \oplus p=0$ for every $p:\Omega$
(where it is unspecified which element of $\Omega$ the zero element of the
group is – it can be $\text{false}$ , $\text{true}$ , or any element of $\Omega$ ).

Now define $f(p) = p \oplus \text{false} \oplus \text{true}$ .

Then we have the following chain of logical equivalences:

$f(p)$

$\iff f(p) = \text{true}$

$\iff p \oplus \text{false} \oplus \text{true} = \text{true}$

$\iff p \oplus \text{false} = 0$

$\iff p = \text{false}$

$\iff \lnot p$ .

Hence $f(p) = \lnot p$ by propositional extensionality (or univalence for propositions, in the case of HoTT/UF).

But $f(p)$ , being a group action, is an automorphism and hence an
involution by Higgs’ theorem (or already by the above consequences of
Higgs’ theorem and direct calculation), which amounts to $\lnot\lnot p = p$ , and
therefore excluded middle holds.

This argument is also written here in Agda, with a weaker assumption, namely that $\Omega$ is given the structure of a left-cancellative monoid, including a proof of Higgs Involution Theorem.

I wouldn’t be surprised if this fact is already available in the literature or the folklore. Is it?

This entry was posted in Uncategorized. Bookmark the permalink.

7 Responses to Can the type of truth values be given the structure of a group?

Martin Escardo says:

12 February 2021 at 18:15

Update: none of the topos theorists we asked, including Peter Johnstone, were aware of the fact that the object of truth values can be a group only in a boolean topos.

- Mamuka Jibladze says:
  
  14 October 2021 at 07:27
  
  Nevertheless, the paper “[Automorphisms of Ω](https://link.springer.com/article/10.1007/BF02488012)” by Johnstone (algebra universalis volume 9, pages1–7 (1979)) is relevant. There he proves the externalization of the fact that the image of the Higgs filter H := { p:Ω | [p,true] = {p,true} } under the map sending p:Ω to p _ is precisely Aut(Ω) = Mono(Ω,Ω), and I believe his arguments actually prove the full-fledged internal version too. Then, a group structure on Ω provides an embedding of Ω into H; composite of this embedding with the inclusion of H into Ω is an embedding of Ω into itself, hence an automorphism, hence the inclusion of H into Ω is epi, hence H contains false, so that Ω = {false, true}.
  
  Your argument is doubtlessly more elementary, though.
  
  - Mamuka Jibladze says:
    
    14 October 2021 at 07:29
    
    Hm, biimplication vanished by some reason…
    
Mamuka Jibladze says:

26 October 2021 at 13:02

Actually already a mono $i:\Omega\to\Omega$ with $i(\mathbf{false})=\mathbf{true}$ implies booleanness. Indeed since $i$ is mono, $i(p)=\mathbf{true}$ implies $p=\mathbf{false}$, so that $i(p)=(p=\mathbf{false})$. Then again since $i$ is mono, $i(p)=i(q)$ implies $p=q$. Taking here $q=((p=\mathbf{false})=\mathbf{false})$ gives (since triple negation coincides with single negation) $((p=\mathbf{false})=\mathbf{false})=p$, i. e. $\neg\neg p = p$, which gives booleanness.

Martin Escardo says:

21 November 2021 at 02:18

Thanks. This argument looks similar to the proof of Theorem 16 of this paper: https://drops.dagstuhl.de/opus/volltexte/2018/9855/

- Mamuka Jibladze says:
  
  21 November 2021 at 08:35
  
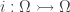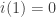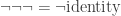  Thanks for the link! It is remarkable – in a sense our assumptions are opposite to each other: we both deal with a mono $i:\Omega\rightarrowtail\Omega$ ; you assume $i(1)=0$ and I $i(0)=1$ . Conclusions are curiously similar yet different: for me, it is that $i=\neg$ , so $latex\neg$ is mono, so one can cancel $\neg\neg\neg=\neg\text{identity}$ from the right, implying that 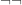$\neg\neg$ is identity. For you, that $latex\neg i$ is identity, so that $latex\neg$ is (a split) epi, hence booleanness by your Lemma 15. The latter, in effect, cancels $\neg\neg\neg=\text{identity}\neg$ from the left!
  
  - Mamuka Jibladze says:
    
    21 November 2021 at 08:41
    
    Oh no I messed it up again! The “left” and “right” must be swapped… Too bad I cannot edit my comments.