Covering spaces are one of the important topics in classical homotopy theory, and this post summarizes what we have done in HoTT. We have formulated the covering spaces and (re)proved the classification theorem based on (right) $\pi_1(X)$ -sets, i.e., sets equipped with (right) group actions of the fundamental group $\pi_1(X)$ . I will explain the definition and why we need some constancy factorization trick in the proof.

Definition

So, what are covering spaces in HoTT? The core ingredient of covering spaces is a fibration, which is easy in HoTT, because every function or dependent type in HoTT can be viewed as a fibration (up to homotopy). The only problem is the possible higher structures accidentally packed into the space (which are usually handled separately in classical homotopy theory). To address this, we have another condition that each fiber is a set. These two conditions together match the classical definition. More precisely, given a base space $X$ , a covering is a mapping $f$ from $X$ to some universe (or, a type family indexed by $X$ ) where for each $x \in X$ we know $f(x)$ is a set.

One can also formulate coverings as mappings instead of type families. I personally prefer the latter because they seem easier to work with in type theory. Note that we did not assert that the base space $X$ is path-connected or pointed, which are required by interesting theorems (ex: the classification theorem) but not by the definition.

Classification Theorem

The classification theorem says there is an isomorphism between $\pi(X,x_0)$ -set and covering spaces. Here we assume $X$ is path-connected and pointed (based) at $x_0 \in X$ .

The direction from covering spaces to $\pi(X,x_0)$ -sets is easier, since the set can simply be the fiber over the point $x_0$ , and the group action can be defined as transporting along an element in the homotopy group. The other direction is more challenging, requiring an explicit construction of the covering space from the given $\pi(X,x_0)$ -set. Naturally, the fiber over $x_0$ should be the underlying set, but what about other fibers? For arbitrary point $x$ in $X$ , due to the connectedness of the base space $X$ , there exists a (truncated) path from $x_0$ to $x$ , which can be used to transport everything in the fiber over $x_0$ to the fiber over $x$ . However, unless the homotopy group is trivial, one needs to identify multiple copies produced by different paths. We simply threw in gluing 1-cells and then made each fiber a set.

The above higher inductive type, which is called ribbon in the library, goes as follows: It is parametrized by the $\pi(X,x_0)$ -set, the underlying set $Y$ , the group action $\bullet$ , and the point $x$ in focus. The trace constructor “copies” everything from the fiber over $x_0$ to the fiber over $x$ along some path in the base type, and the paste constructor glues multiple copies made by different paths.

data ribbon (Y : Set) (∙ : Action Y) (x : X) : Set where
  trace : Y → Truncated 0 (x₀ = x) → ribbon x
  paste : (y : Y) → (loop : Truncated 0 (x₀ = x₀))
        → (p : Truncated 0 (x₀ = x))
        → trace (y ∙ loop) p ≡ trace y (loop ∘ p)

The most interesting part is to show that creating ribbons is left inverse to constructing $G$ -sets as mentioned in the beginning of the section. It suffices to show that ribbons indeed form the original covering space, which is, by functional extensionality, equivalent to demonstrating that they are fiberwise equivalent. The trouble is that, for a point $x \in X$ and a point $y$ in the fiber of the input covering over $x$ , one needs a path $x_0 = x$ to even make one point in the ribbon; while we can get a $(-1)$ -truncated path out of the connectedness condition, the constructor requires a $0$ -truncated path.

The constancy comes to rescue! It can be shown that, if there is a function $f$ from $A$ to a set $B$ , and $f$ is constant, then $f$ factors through $|A|$ with ideal computational behaviors. In our case, different points generated by different paths will be glued together by the paste constructor and moreover each fiber is a set. Therefore we can apply this lemma to establish the fiberwise equivalence, and hence the theorem!

Remarks

We also proved that the homotopy group itself corresponds to the universal covering, where universality is defined as being simply-connected. The ribbon construction, as an explicit description for covering spaces, comes in handy. In addition, we calculated $\pi(S^1)$ (again) with the new library; however, even with aggressive Agda optimization, the complexity remains—one still needs to prove the contractibility of some covering of $S^1$ for universality. Perhaps there are other better examples which can show the real power of this isomorphism?

The Agda code is currently available at http://hott.github.io/HoTT-Agda/Homotopy.Cover.HomotopyGroupSetIsomorphism.html but we are rebuilding the whole library. This link might not be valid after the migration.

5 Responses to Covering Spaces

jessemckeown says:

30 April 2013 at 12:19

Well, I like!
Some rambling thoughts;
1) It should not be *too* hard to adapt this ribbon to define the $n$ th Moore-Postnikov layer of a map $A \to B$ , though perhaps the desired properties of Moore-Postnikov towers will still be difficult?

2) The present note and previous rambling thought make me wish also for a general delooping construction, because really the universal cover is the delooping of the identity-component of the first loopspace; but, then, coherence… for things of bounded hlevel, oughtn’t coherence to be bounded, too? For instance, the present construction really is delooping an action on an hlevel-0 thing.

3) Why should $\latex \pi_1(S^1)$ be so difficult? Apart from how homology and homotopy don’t really get along, I mean, which is enough; Every connected pointed space, of course, has a contractible fibration over it, in $\Sigma_p (\gamma : p \sim p_0)$ , and ideally a calculation of $\pi_1(S^1)$ should reduce to arguing that this is a covering map in the case of the circle; and that should reduce to arguing that $S^1$ is hlevel-small… hlevel-2?

4) Of course, a really-internally-clever algebraic topology assistant would recognize that the presentation of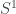 $S^1$ as a point with an extra equation is a *small* presentation, but not a very *smooth* one, and work-out the better presentation having
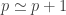
* A copy of Z
* for each $z : Z$ , a path $[z] \simeq [z+1]$
* lift the $+$ action of Z on itself to that
* for each $p$ , a path $p \simeq p + 1$
Then there is some argument to run that this is equivalent to the circle… OK, I must modify that thought: expecting a machine to recognize that a presentation is not smooth is a bit much; but it should give you the option of smoothing-out in an automated way, which the user can then make use of when it helps.

5) Actually, that kind of presentation-replacement seems to be how I actually think of using universal covers. It’s a pitty the word problem is unsolvable…

- favonia says:
  
  30 April 2013 at 15:32
  
  Hi! Sorry that I’m still learning the terminology in homotopy theory, but I’ll take a look at the Postnikov tower and others. I can answer (3) right now: No, the calculation is not difficult; we already have 3~4 calculations of $\pi_1(S_1)$ in different styles, and some of them are under 150 lines of code. It’s just a little bit disappointing (to me) that the library cannot further simply calculation of $\pi_1(S_1)$ to, say, 100 or fewer lines. I had some higher expectation. 🙂
  
  - Guillaume Brunerie says:
    
    2 May 2013 at 16:29
    
    In the upcoming new Agda library, I already have two proofs of $latex\pi_1(S^1)=\mathbb{Z}$ (encode-decode and flattening lemma) and they are both under 100 lines of code (excluding library code). The flattening lemma proof is a bit shorter, but uses much more library code. See https://github.com/HoTT/HoTT-Agda/blob/2.0/homotopy/LoopSpaceCircle.agda
    
    - Guillaume Brunerie says:
      
      2 May 2013 at 23:11
      
      I know added a third proof (closer to Mike’s original proof) which is ~105 lines long (same link).
      
- Bas Spitters says:
  
  2 May 2013 at 04:38
  
  We have something close to Moore-Postnikov
  [http://uf-ias-2012.wikispaces.com/file/view/images.pdf/401765624/images.pdf](here)
  
  I will think about the precise formulation.