(Post by Brent Yorgey)
My dissertation was on the topic of combinatorial species, and specifically on the idea of using species as a foundation for thinking about generalized notions of algebraic data types. (Species are sort of dual to containers; I think both have intereseting and complementary things to offer in this space.) I didn’t really end up getting very far into practicalities, instead getting sucked into a bunch of more foundational issues.
To use species as a basis for computational things, I wanted to first “port” the definition from traditional, set-theory-based, classical mathematics into a constructive type theory. HoTT came along at just the right time, and seems to provide exactly the right framework for thinking about a constructive encoding of combinatorial species.
For those who are familiar with HoTT, this post will contain nothing all that new. But I hope it can serve as a nice example of an “application” of HoTT. (At least, it’s more applied than research in HoTT itself.)
Combinatorial Species
Traditionally, a species is defined as a functor , where
is the groupoid of finite sets and bijections, and
is the category of finite sets and (total) functions. Intuitively, we can think of a species as mapping finite sets of “labels” to finite sets of “structures” built from those labels. For example, the species of linear orderings (i.e. lists) maps the finite set of labels
to the size-
set of all possible linear orderings of those labels. Functoriality ensures that the specific identity of the labels does not matter—we can always coherently relabel things.
Constructive Finiteness
So what happens when we try to define species inside a constructive type theory? The crucial piece is : the thing that makes species interesting is that they have built into them a notion of bijective relabelling, and this is encoded by the groupoid
. The first problem we run into is how to encode the notion of a finite set, since the notion of finiteness is nontrivial in a constructive setting.
One might well ask why we even care about finiteness in the first place. Why not just use the groupoid of all sets and bijections? To be honest, I have asked myself this question many times, and I still don’t feel as though I have an entirely satisfactory answer. But what it seems to come down to is the fact that species can be seen as a categorification of generating functions. Generating functions over the semiring can be represented by functions
, that is, each natural number maps to some coefficient in
; each natural number, categorified, corresponds to (an equivalence class of) finite sets. Finite label sets are also important insofar as our goal is to actually use species as a basis for computation. In a computational setting, one often wants to be able to do things like enumerate all labels (e.g. in order to iterate through them, to do something like a map or fold). It will therefore be important that our encoding of finiteness actually has some computational content that we can use to enumerate labels.
Our first attempt might be to say that a finite set will be encoded as a type together with a bijection between
and a canonical finite set of a particular natural number size. That is, assuming standard inductively defined types
and
,
However, this is unsatisfactory, since defining a suitable notion of bijections/isomorphisms between such finite sets is tricky. Since is supposed to be a groupoid, we are naturally led to try using equalities (i.e. paths) as morphisms—but this does not work with the above definition of finite sets. In
, there are supposed to be
different morphisms between any two sets of size
. However, given any two same-size inhabitants of the above type, there is only one path between them—intuitively, this is because paths between
-types correspond to tuples of paths relating the components pointwise, and such paths must therefore preserve the particular relation to
. The only bijection which is allowed is the one which sends each element related to
to the other element related to
, for each
.
So elements of the above type are not just finite sets, they are finite sets with a total order, and paths between them must be order-preserving; this is too restrictive. (However, this type is not without interest, and can be used to build a counterpart to L-species. In fact, I think this is exactly the right setting in which to understand the relationship between species and L-species, and more generally the difference between isomorphism and equipotence of species; there is more on this in my dissertation.)
Truncation to the Rescue
We can fix things using propositional truncation. In particular, we define
That is, a “finite set” is a type together with some hidden evidence that
is equivalent to
for some
. (I will sometimes abuse notation and write
instead of
.) A few observations:
- First, we can pull the size
out of the propositional truncation, that is,
. Intuitively, this is because if a set is finite, there is only one possible size it can have, so the evidence that it has that size is actually a mere proposition.
- More generally, I mentioned previously that we sometimes want to use the computational evidence for the finiteness of a set of labels, e.g. enumerating the labels in order to do things like maps and folds. It may seem at first glance that we cannot do this, since the computational evidence is now hidden inside a propositional truncation. But actually, things are exactly the way they should be: the point is that we can use the bijection hidden in the propositional truncation as long as the result does not depend on the particular bijection we find there. For example, we cannot write a function which returns the value of type
corresponding to
, since this reveals something about the underlying bijection; but we can write a function which finds the smallest value of
(with respect to some linear ordering), by iterating through all the values of
and taking the minimum.
- It is not hard to show that if
, then
is a set (i.e. a 0-type) with decidable equality, since
is equivalent to the 0-type
. Likewise,
itself is a 1-type.
- Finally, note that paths between inhabitants of
now do exactly what we want: a path
is really just a path
between 0-types, that is, a bijection, since
trivially.
Constructive Species
We can now define species in HoTT as functions of type . The main reason I think this is the Right Definition ™ of species in HoTT is that functoriality comes for free! When defining species in set theory, one must say “a species is a functor, i.e. a pair of mappings satisfying such-and-such properties”. When constructing a particular species one must explicitly demonstrate the functoriality properties; since the mappings are just functions on sets, it is quite possible to write down mappings which are not functorial. But in HoTT, all functions are functorial with respect to paths, and we are using paths to represent the morphisms in
, so any function of type
automatically has the right functoriality properties—it is literally impossible to write down an invalid species. Actually, in my dissertation I define species as functors between certain categories built from
and
, but the point is that any function
can be automatically lifted to such a functor.
Here’s another nice thing about the theory of species in HoTT. In HoTT, coends whose index category are groupoids are just plain -types. That is, if
is a groupoid,
a category, and
, then
. In set theory, this coend would be a quotient of the corresponding
-type, but in HoTT the isomorphisms of
are required to correspond to paths, which automatically induce paths over the
-type which correspond to the necessary quotient. Put another way, we can define coends in HoTT as a certain HIT, but in the case that
is a groupoid we already get all the paths given by the higher path constructor anyway, so it is redundant. So, what does this have to do with species, I hear you ask? Well, several species constructions involve coends (most notably partitional product); since species are functors from a groupoid, the definitions of these constructions in HoTT are particularly simple. We again get the right thing essentially “for free”.
There’s lots more in my dissertation, of course, but these are a few of the key ideas specifically relating species and HoTT. I am far from being an expert on either, but am happy to entertain comments, questions, etc. I can also point you to the right section of my dissertation if you’re interested in more detail about anything I mentioned above.
Thanks for this nice post, Brent — looking forward to studying your thesis!
I think the theory of species has a lot of potential as an application for HoTT.
Very cool! I agree, this is an area of math thath is just crying out to be done univalently.
Have you tried formalizing any of the theory of species in a proof assistant? Some of the basic theory of finite sets is already formalized in the HoTT/Coq library.
Regarding “why finite sets”, I’ve always thought that that’s just “what species are about”. They’re called combinatorial species, and I’ve always seen them presented as being about counting the ways to give certain structure to finite sets (which is, roughly speaking, what “combinatorics” is about). I guess you have other applications in mind, though.
Thanks! I haven’t tried formalizing any of this, though I’ve certainly thought about it, and I think it would be really worthwhile. I think Dan Licata had a student who was planning to try working on this but I don’t know how far they got.
I agree with you re: “why finite sets” and combinatorics. Perhaps a better way to ask the question I am really asking is: what, if anything, do we *lose* if we drop the “finite” restriction? Or put conversely, where does the theory of species make use of finiteness in an essential way? This is one question a proof assistant formalization would really help answer.
Nice!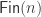 , is equivalent to the natural numbers. This is because the first component (a type
, is equivalent to the natural numbers. This is because the first component (a type 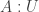 ) and the third component (an equality
) and the third component (an equality  ) form a “singleton pair” and cancel each other out; see the HoTT book Lemma 3.11.8.
) form a “singleton pair” and cancel each other out; see the HoTT book Lemma 3.11.8.
A small comment: The type that you discuss in the paragraph “Constructive Finiteness”, i.e. the type of types that are equivalent to some
Ah, thanks for the comment! That is a much easier way to understand why this is not the type we want.
Pingback: Combinatorial species and finite sets in #HoTT | Henosophia TOPOSOPHIA μαθεσις uni√ersalis τοποσοφια MATHESIS οντοποσοφια ενοσοφια Philosophie, théorie des catégories et théorie homotopique des types