Real-cohesive homotopy type theory

Posted on 25 September 2015 by Mike Shulman

Two new papers have recently appeared online:

Brouwer’s fixed-point theorem in real-cohesive homotopy type theory by me, and
Adjoint logic with a 2-category of modes, by Dan Licata with a bit of help from me.

Both of them have fairly chatty introductions, so I’ll try to restrain myself from pontificating at length here about their contents. Just go read the introductions. Instead I’ll say a few words about how these papers came about and how they are related to each other.

Cohesive homotopy type theory is something that I’ve been working on with Urs Schreiber since some 3-4 years ago, involving an adjoint string of modalities ʃ $\dashv \flat\dashv \sharp$ that internalizes Lawvere’s axiomatic cohesion. We wrote a little note about it. About a year ago, I started to wonder whether cohesive HoTT could solve “the problem of the two circles”. By this I mean the fact that in HoTT we have both the higher inductive circle, generated by a point base and an equality loop : base = base, and the topological circle, defined for instance as $\{ (x,y)\in \mathbb{R}^2 \mid x^2+y^2=1 \}$ . The former is a 1-type that has “only one point” (to be precise, it is 0-connected), whereas the latter is a 0-type (a set) that has infinitely many distinct points. The “problem” is, how are these two circles related?

In March I gave a talk about this at CMU, in which I introduced an enhancement of cohesive HoTT called “real-cohesive HoTT” and proved in it that the “shape” ʃ (the cohesive incarnation of the fundamental $\infty$ -groupoid) of the topological circle is the homotopical circle. At that point Dan Licata, who was in the audience, got interested and started convincing me to look for a better way to formulate cohesion type-theoretically.

The problem with cohesive type theory is that the comodality $\flat$ , unlike the modalities ʃ and $\sharp$ , can’t be described internally as a map $\mathrm{Type}\to \mathrm{Type}$ with properties. Urs and I first noticed this semantically; later I proved a no-go theorem internally (see section 4 of the real-cohesion paper). Urs and I worked around this by representing $\flat$ as a map $\sharp \mathrm{Type}\to \sharp\mathrm{Type}$ ; while later, I started experimenting with using Coq’s modules to restrict the context. But in March Dan told me about modal type theories due to Pfenning-Davies and Reed, in which a segregation of the context limits the applicability of modal type formers. The existing work had focused on more traditional modalities such as necessity $\Box$ and possibility $\lozenge$ , but Dan thought there ought to be a version that would work for the cohesive modalities as well.

There followed a very productive back-and-forth in which Dan developed the metatheory with an eye towards a proof-theoretically well-behaved calculus, while I cast around for a version of the theory that would make for a perspicuous presentation of real-cohesion. We ended up with an idea for a very general kind of “adjoint type theory”, which is not yet worked out in full; the real-cohesion paper uses only one particular case of it, while the adjoint logic paper develops the metatheory of the general case but in a very simplified way (no dependent types and only one-variable contexts).

Dan coded up a simple sequent calculus for this theory in Agda and proved some nice theorems about it. Meanwhile I generalized it to dependent type theory in the special case of cohesion and used it to write up the two circles theorem, and also a synthetic version of the classical homotopy-theoretic proof of Brouwer’s fixed-point theorem as a proof of concept. I’m very excited about real-cohesion, and also adjoint type theory more generally; I think it has a lot of untapped potential. A few possibilities are mentioned in the paper.

Unfortunately there is one fly in the ointment: cohesive type theory done in this way can’t be formalized directly in existing proof assistants. One can describe the theory using a proof assistant as the metatheory, of course. For actually proving things in the theory, this works pretty well for basic theorems in a 1-variable sequent calculus (see the Agda code accompanying the adjoint logic paper), but for more complicated results in a richer language it would become quite tedious, running into the common problems with representing languages with variable binding and dependent types. At one point I entertained notions that Coq’s modules would help; but at the moment I’m kind of down on that idea because modules have a lot of “features” that make them at best annoying to use in this way (which, to be fair, is not at all how they were intended to be used). So formalization may have to wait until someone implements an adjoint-type-theory proof assistant directly. (Anyone developing a proof assistant feel like incorporating it?)

This entry was posted in Applications, Foundations, Paper. Bookmark the permalink.

13 Responses to Real-cohesive homotopy type theory

Daniel R. Grayson says:

30 September 2015 at 21:40

This is interesting! In your paper, you refer to topological ∞-groupoids on page 5 and the following pages as the objects of the intended model. May I also think of those as simplicial objects in the category of topological spaces?

Reply
- Mike Shulman says:
  
  30 September 2015 at 22:55
  
  For purposes of intuition, I would say yes, with some caveats. Firstly, of course they need to be “fibrant” in order to be any sort of ∞-groupoid. Secondly, even if they are all fibrant, I expect that simplicial maps will be too strict and you’ll need some sort of anafunctory business to get the right “topological ∞-functors”. And thirdly, as mentioned in section 7, topological spaces are all concrete, whereas to be topos-like we need some non-concrete objects too.
  
  Reply
saizan says:

2 October 2015 at 04:15

This is very interesting and looks much more accessible to a type theorist than previous work on cohesion. From that same point of view it also feels very unnatural to give some special status to the reals, but fair enough.

You discuss how this compares with the topology from Johnstone’s topological topos, do you also know how these modalities would compare with parametricity? considering that reflexive graphs are a cohesive topos.

Reply
- Mike Shulman says:
  
  2 October 2015 at 10:53
  
  Glad to hear it! Note that very few of the results in the paper depend on giving the reals any special status; only in the very last sections 11-12 is the full strength of that assumption used. Part 1 is about “spatial type theory” which involves no axioms at all and describes the adjoint modalities $\flat \dashv\sharp$ using “adjoint logic”, and the first few sections of Part 2 are mostly about cohesion more generally than real-cohesion, using three successively stronger axioms C0, C1, and C2 none of which give any special status to the reals.
  
  I don’t know of any way in which the cohesive structure of reflexive graphs is related to parametricity. My understanding is that parametricity is (in one of the simplest cases) about a section of the forgetful functor RGraph → Type that is itself a “logical functor” (i.e. preserves all the topos structure); whereas cohesion is about the left and right adjoints of that forgetful functor, neither of which is logical. Is there any connection?
  
  Reply
  - Andrea Vezzosi says:
    
    2 October 2015 at 12:30
    
    I guess I haven’t seen the modalities explicitly used for it, but they seem relevant.
    Standard parametricity results like the encoding of initial algebras rely on the “identity extension” lemma, or how the relational component of some F : U -> U is going to send the equality relation to the equality relation.
    
    In the following they show that RGraph is a cwf and then define U as the universe of discrete graphs to obtain the identity extension lemma.
    
    http://bentnib.org/dtt-parametricity.html
    
    I’ve found the ʃ modality useful to make things fit in U, and it seems you can use it to get some invariance results, like showing the functions U -> Bool are constant, because Bool is discrete, if you internalize that ʃU = 1.
    
    I wonder though if this is going to scale, U itself is not discrete, so it seems like this approach singles out a bottom level? What if I want to enforce invariance properties for terms that define types? So I’d like to have more perspectives on this.
    
    Reply
    - Mike Shulman says:
      
      2 October 2015 at 12:36
      
      What’s the value of using reflexive graphs? If you use not-necessarily-relexive graphs, don’t you get a universe of all graphs?
      
      Reply
      - Andrea Vezzosi says:
        
        2 October 2015 at 12:50
        
        The value is for the identity extension lemma. The F : U -> U is forced to be equality-preserving because it is respecting the reflexivity map of U.
        
        Reply
        
        Mike Shulman says:
        
        2 October 2015 at 19:07
        
        Hmm… maybe I’m not sure what “equality-preserving” means. The extent of my knowledge about parametricity is about this.
        
        But in any case, there is also a universe of all reflexive graphs (since reflexive graphs are a topos), even if it doesn’t have as nice an internal description.
        
        Reply
        
        Andrea Vezzosi says:
        
        3 October 2015 at 07:52
        
        Yes, there is a universe of all reflexive graphs, let’s call it V as opposed to U from before, but regardless of descriptions it seems that some parametricity properties we expect do not hold if you use V to replace Haskell’s or System F’s *.
        
        This is not a problem for the parametricity result about (X : *) -> X -> X, because in its proof you explicitly know all the predicates/relations involved, since you pick what to use for X.
        
        But in the proof that, for some arbitrary strong functors F, G : * -> * the type (X : *) -> F X -> G X is the one of natural transformations you don’t know how the relations generated by the witnesses for F and G compare with equality at F and G so you get stuck.
        
        An (F : * -> *) is equality preserving when the witness that F sends relations to relations, in particular sends the equality relation to the equality relation. If F and G above are equality-preserving we can show that the naturality square commutes.
        
        The original identity extension lemma (from Reynolds) says that all the type expressions in System F are equality preserving. In the RGraph model the maps U -> U are equality preserving as well, but the maps V -> V are not necessarily so.
        
        Reply
  - Mike Shulman says:
    
    4 October 2015 at 07:46
    
    Okay, I still don’t fully understand the reflexive-graphs thing, but I have a guess at why my intuition was wrong: I’m used to inverse-diagram models like unary or binary relations, where the universe V of all diagrams has the property that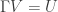 $\Gamma V = U$ , i.e. its underlying type is the universe of types. But for models like reflexive graphs that fails, so now I can sort of see why you might want to use the universe of discrete types instead.
    
    I still don’t think I can answer your question about “scaling”, though.
    
    Reply
    - Andrea Vezzosi says:
      
      4 October 2015 at 11:18
      
      Ah, yeah, the intuitions change a lot with the reflexivity map, for exponentials and universes.
      Meanwhile I’ve found an example where “polymorphic functions are natural” is actually false if you are allowed 2 universes and equality:
      http://lpaste.net/142204
      
      Fair enough about the scaling question.
      
      Reply
spitters37 says:

3 October 2015 at 15:47

Just to be sure the [topos of reflexive graphs is cohesive](http://ncatlab.org/nlab/show/cohesive+topos#Graphs). Andrea, I believe we chatted about this connection in Chalmers.

Reply
Pingback: Differential Geometry in Modal HoTT | Homotopy Type Theory