Exercise 6.9 of the HoTT book tells us that, and assuming LEM, we can exhibit a function such that
is a non-identity function
I have proved the converse of this. Like in exercise 6.9, we assume univalence.
Parametricity
In a typical functional programming career, at some point one encounters the notions of parametricity and free theorems.
Parametricity can be used to answer questions such as: is every function
f : forall x. x -> x
equal to the identity function? Parametricity tells us that this is true for System F.
However, this is a metatheoretical statement. Parametricity gives properties about the terms of a language, rather than proving internally that certain elements satisfy some properties.
So what can we prove internally about a polymorphic function ?
In particular, we can see that internal proofs (claiming that must be the identity function for every type
) cannot exist: exercise 6.9 of the HoTT book tells us that, assuming LEM, we can exhibit a function
such that
is
(Notice that the proof of this is not quite as trivial as it may seem: LEM only gives us
if
is a (mere) proposition (a.k.a. subsingleton). Hence, simple case analysis on
does not work, because this is not necessarily a proposition.)
And given the fact that LEM is consistent with univalent foundations, this means that a proof that is the identity function cannot exist.
I have proved that LEM is exactly what is needed to get a polymorphic function that is not the identity on the booleans.
Theorem. If there is a function with
then LEM holds.
Proof idea
If then by simply trying both elements
we can find an explicit boolean
such that
Without loss of generality, we can assume
For the remainder of this analysis, let be an arbitrary proposition. Then we want to achieve
to prove LEM.
We will consider a type with three points, where we identify two points depending on whether holds. In other words, we consider the quotient of a three-element type, where the relation between two of those points is the proposition
I will call this space and it can be defined as
where
is the suspension of
This particular way of defining the quotient, which is equivalent to a quotient of a three-point set, will make case analysis simpler to set up. (Note that suspensions are not generally quotients: we use the fact that
is a proposition here.)
Notice that if holds, then
and also
We will consider at the type
(not
itself!). Now the proof continues by defining
(where is the equivalence given by the identity function on
) and doing case analysis on
and if necessary also on
for some elements
I do not believe it is very instructive to spell out all cases explicitly here. I wrote a more detailed note containing an explicit proof.
Notice that doing case analysis here is simply an instance of the induction principle for In particular, we do not require decidable equality of
(which would already give us
which is exactly what we are trying to prove).
For the sake of illustration, here is one case:
Assume
holds. Then since
then by transporting along an appropriate equivalence (namely the one that identifies
with
we get
But since
is an equivalence for which
is a fixed point,
must be the identity everywhere, that is,
which is a contradiction.
I formalized this proof in Agda using the HoTT-Agda library
Acknowledgements
Thanks to Martín Escardó, my supervisor, for his support. Thanks to Uday Reddy for giving the talk on parametricity that inspired me to think about this.
From reading the Agda proof (thanks for linking to it!), it seems that this result can be informally stated as
If you have enough introspection power into polynomorphic types to create a non-identity type (at 2), then you have enough power to decide all (mere) propositions.
In other words, this tells you a lot about syntactic codes for Universes, aka reflection. If you build in sufficient reflection that you can pattern-match on your types, you’ve already built in LEM. Which is a very cool result.
That is a nice way of looking at it, thanks.
What can be said if there is , and an inhabited type
, and an inhabited type  with
with 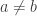 and such that
and such that  has no fixed points:
has no fixed points:  ?
?
Very cool!
One thought that may be worth mentioning: I think that if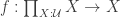 , then in fact
, then in fact  must be an equivalence. For there are only four functions
must be an equivalence. For there are only four functions 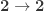 , and the two that are not equivalences (the constant functions) are not preserved by
, and the two that are not equivalences (the constant functions) are not preserved by  . Thus, if
. Thus, if  is not the identity, then it is
is not the identity, then it is  , and so we necessarily have both
, and so we necessarily have both 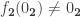 and
and 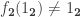 .
.
Also, I wonder whether your case analyses could be simplified by starting with instead of
instead of 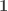 ? The crucial ingredients seem to be
? The crucial ingredients seem to be
Now consider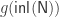 and
and 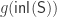 . If either of them lands in
. If either of them lands in  , then
, then 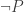 by the first observation above. Thus it remains to consider the case when both land in
by the first observation above. Thus it remains to consider the case when both land in 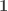 ; but then since
; but then since  is an equivalence,
is an equivalence,  and hence
and hence  .
.
I haven’t tried to formalize this, though, so I could have missed something.
I agree the result is very cool! And I agree with Andrej that there are more questions to be answered.
When Auke conjectured the result, I was a bit skeptical, but at the same time hopeful. He found a proof in a few days after his conjecture, which was very nice and impressive.
The essence of Auke’s argument is to construct a space whose number of points depends on a given proposition , being
, being  if
if  holds, but something else otherwise, forcing
holds, but something else otherwise, forcing  to rely on a conundrum that can only be solved by an oracle for excluded middle.
to rely on a conundrum that can only be solved by an oracle for excluded middle.
Given this analysis of his construction/argument, the space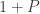 also fits the bill: It has two points if
also fits the bill: It has two points if  holds, and one point if it doesn’t. So in general we can’t know how many points it has. In particular, this gives a difficult time to the function
holds, and one point if it doesn’t. So in general we can’t know how many points it has. In particular, this gives a difficult time to the function  which wants
which wants 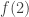 to be the flip function.
to be the flip function.
To see this, consider .
.
Again like Auke did, we check whether this lands on the right or the left:
* If it lands on the left, we conclude that can’t hold, because if it
can’t hold, because if it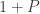 would be
would be  , by univalence, which means that
, by univalence, which means that  would
would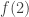 , landing on the right, which contradicts
, landing on the right, which contradicts
did then
also need to flip, like
the hypothesis that we landed on the left.
* If it lands on the right, we conclude directly that holds.
holds.
Hence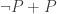 , as required.
, as required.
We have used the same ingredients and ideas as in Auke’s original proof.
But we managed to get rid of quotients. We can get rid of univalence, as already emphasized by Auke himself, by just requiring that be invariant under equivalences, which can be regarded as an extensionality requirement.
be invariant under equivalences, which can be regarded as an extensionality requirement.
In this way, we get Auke’s Theorem in the following generality: in intensional MLTT, if there is a polymorphic, extensional as above that flips the booleans, then excluded middle holds.
as above that flips the booleans, then excluded middle holds.
Very nice. Here is I think a further generalization. Suppose is polymorphic and extensional, and that there is a type
is polymorphic and extensional, and that there is a type  such that
such that 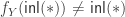 . Now for any proposition
. Now for any proposition  , let
, let  and consider
and consider  . If it is
. If it is 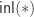 , then
, then 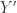 cannot be equivalent to
cannot be equivalent to  by an equivalence that preserves the coproduct decompositions; hence
by an equivalence that preserves the coproduct decompositions; hence 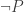 . But if it is
. But if it is  then
then 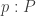 .
.
In other words, we get LEM as soon as a polymorphic extensional function has a detachable non-fixed-point.
It seems one cannot learn about this proof without learning this generalization, as Martin and I also both found this.
There are also a couple of immediate results with boolean-valued polymorphic extensional functions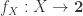 : for example, it is easy to prove that for a homogeneous type
: for example, it is easy to prove that for a homogeneous type  (that is, a type such that for
(that is, a type such that for  , there is an automorphism of
, there is an automorphism of  that swaps
that swaps  and
and  ), if
), if  is non-constant, then bottom (rather than merely a taboo).
is non-constant, then bottom (rather than merely a taboo).
I think we can probably generalize further by replacing by any inhabited type. That is, suppose
by any inhabited type. That is, suppose  and
and  such that
such that 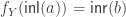 for some
for some  . Then put
. Then put 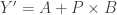 and consider
and consider 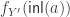 and argue similarly.
and argue similarly.
Pingback: Parametricity, automorphisms of the universe, and excluded middle | Homotopy Type Theory
Pingback: Model of the circle without HITs – Math Solution