Eilenberg-MacLane Spaces in HoTT

For those of you who have been waiting with bated breath to find out what happened to your favorite characters after the end of Chapter 8 of the HoTT book, there is now a new installment:

Eilenberg-MacLane Spaces in Homotopy Type Theory
Dan Licata and Eric Finster
To appear at LICS 2014; pre-print available here.
Agda available here.

Homotopy type theory is an extension of Martin-Lof type theory with principles inspired by category theory and homotopy theory. With these extensions, type theory can be used to construct proofs of homotopy-theoretic theorems, in a way that is very amenable to computer-checked proofs in proof assistants such as Coq and Agda. In this paper, we give a computer-checked construction of Eilenberg-MacLane spaces. For an abelian group G, an Eilenberg-MacLane space K(G,n) is a space (type) whose nth homotopy group is G, and whose homotopy groups are trivial otherwise. These spaces are a basic tool in algebraic topology; for example, they can be used to build spaces with specified homotopy groups, and to define the notion of cohomology with coefficients in G. Their construction in type theory is an illustrative example, which ties together many of the constructions and methods that have been used in homotopy type theory so far.

The Agda formalization of this result was actually done last spring at IAS; the only thing new in the paper is the “informalization” of it. This write-up would have gone in Chapter 8 of the book, but we ran out of time on the book before writing it up. Overall, I like how this example builds on and ties together a bunch of different techniques and lemmas (e.g. encode-decode gets used a few different times; Peter Lumsdaine’s connectedness lemmas that went into the proof of the Freudenthal suspension theorem gets used, as does Freudenthal itself). When doing the proof, it was kind of fun to actually get to use some lemmas, since most of the previous proofs had required inventing and developing large chunks of library code.

7 Responses to Eilenberg-MacLane Spaces in HoTT

Mike Shulman says:

15 April 2014 at 15:02

Exciting! I look forward to finding the time to read it. Maybe we can get this into the second edition of the book.

Steve Awodey says:

15 April 2014 at 15:20

Congratulations on the LICS acceptance — that makes the third year in a row that there’s been a HoTT paper at LICS!

Mike Shulman says:

12 June 2014 at 19:12

Somewhat belatedly, I finally had a chance to look at this and think about it. It’s very nice!

You mention in several places that a “pointed, 0-connected 1-type” is “like K(G,1)”. But isn’t a pointed, 0-connected 1-type A necessarily equivalent to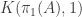 $K(\pi_1(A),1)$ ? The recursion principle of the latter should give a map 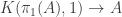$K(\pi_1(A),1)\to A$ , which should be an equivalence by Whitehead’s theorem for 1-types.

- Dan Licata says:
  
  13 June 2014 at 05:14
  
  Good point! That should have occurred to me when writing the paper, but I didn’t think that aspect of the proof through again since proving Whitehead. I wonder if the pi2 = pi1 part of the theorem would be simpler if we did it directly for K(G,1)? it seemed like the “pointed, 0-connected, 1-type, h-structure” stuff was exactly what you needed to get that to go through.
  
  - Mike Shulman says:
    
    13 June 2014 at 10:07
    
    Did you really need $A$ to be a 1-type for that proof? It ought to be true more generally that if A is pointed and 0-connected, then $\pi_2(\Sigma A)$ is the abelianization of $\pi_1(A)$ .
    
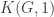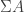    In fact, I think that can be proven from your construction of EM spaces. First show that $\mathrm{Map}_*(K(G,1),K(H,1)) \cong \mathrm{Hom}(G,H)$ by the universal property of $K(G,1)$ , then induct up to show $\mathrm{Map}_*(K(G,n),K(H,n)) \cong \mathrm{Hom}(G,H)$ . Now since $A$ 0-connected implies $\Sigma A$ is 1-connected, we have 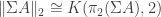$\Vert \Sigma A \Vert_2 \cong K(\pi_2(\Sigma A),2)$ . 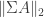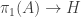But pointed maps from $\Vert \Sigma A \Vert_2$ into $K(H,2)$ are equivalent to pointed maps from $A$ into $\Omega K(H,2) = K(H,1)$ , hence homomorphisms $\pi_1(A) \to H$ , so $\pi_2(\Sigma A)$ must be the reflection of $\pi_1(A)$ into abelian groups. 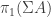(A similar argument should show that for any pointed $A$ , $\pi_1(\Sigma A)$ is the free abelian group on the pointed set $\pi_0(A)$ .)
    
Juan Ospina says:

3 November 2014 at 20:09

It is possible to obtain the Khovanov homotopy types in the context of the Homotopy Type Theory?

Tara says:

23 December 2022 at 02:10

Grreat blog you have