I have adapted Dan Licata’s Agda proof that the higher homotopy groups are abelian to Coq, and I have added a link to the code on the code page of this blog.
Categories
Archives
- October 2023
- January 2023
- June 2022
- March 2022
- December 2021
- March 2021
- January 2021
- November 2020
- October 2020
- January 2020
- May 2019
- March 2019
- February 2019
- December 2018
- November 2018
- August 2018
- June 2018
- May 2018
- March 2018
- November 2017
- October 2017
- September 2017
- January 2017
- October 2016
- September 2016
- July 2016
- February 2016
- January 2016
- December 2015
- September 2015
- August 2015
- July 2015
- June 2015
- January 2015
- December 2014
- November 2014
- September 2014
- August 2014
- June 2014
- April 2014
- March 2014
- February 2014
- December 2013
- October 2013
- August 2013
- July 2013
- June 2013
- May 2013
- April 2013
- March 2013
- February 2013
- November 2012
- September 2012
- August 2012
- June 2012
- May 2012
- April 2012
- March 2012
- January 2012
- December 2011
- November 2011
- July 2011
- April 2011
- March 2011
Blogroll
Meta
Nice! It looks simpler than I expected. I’m intrigued by your comment in the source that proving
adjust_l(and, I presume,adjust_r) byinductiondidn’t give a term that was explicit enough. I’ve had a similar experience with theinductionproofs ofequiv_inv,equiv_inv_is_section, andequiv_inv_is_retraction, but I thought that maybe I was doing something wrong. It’s too bad if the convenient induction tactic has a tendency to produce proofs that aren’t good enough for further use. Are the proofs “really” different, or is Coq just not able to figure out that they’re the same?I also have to repeat my suggestion that we say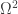 rather than
rather than 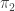 when that’s what we really mean. (-:
when that’s what we really mean. (-:
Thanks, Mike.
In fact, I was just able to prove the two proofs (i.e. paths) are homotopic to one another; see the code below.
What’s going on is that when it comes to Omega^2, the two endpoints of a path p are the same; so induction over p no longer works, and it become impossible to simplify j terms over paths. So one needs a description of the homotopy that doesn’t require unpacking a j-term.
The fact that “proofs” are far from irrelevant here — e.g. they can describe paths that one wants to reason about — makes me uneasy. The particularities of a proof can have an effect on future developments in ways that I still don’t fully understand. For example, Dan pointed out to me that his code only needs one “adjustment” (whereas I need adjust_l and adjust_r) because he used a different definition of concatenation/transitivity than Andrej did. Roughly, Andrej (proved transitivity “trans p q”) / (defined concatenation “p @ q”) by contracting both p and q, which has the effect that “id_path x @ idpath_x” is definitionally equal to “idpath x”. But if you prove it instead by contracting only the first, say, then you get the more useful property that “id_path x @ p” is definitionally equal to “p”. That better definition would have made my code a bit shorter.
Welcome to the wonderful world of proof relevance.
*****
Lemma adjust_l {A} {x y : A} {p q : x ~~> y} (R : p ~~> q) :
idpath x @ p ~~> idpath x @ q.
Proof. exact (idpath_left_unit p @ R @ !(idpath_left_unit q)). Defined.
(* induction R doesn’t given a term that is explicit enough. *)
Lemma adjust_l2 {A} {x y : A} {p q : x ~~> y} (R : p ~~> q) :
idpath x @ p ~~> idpath x @ q.
Proof. induction R. apply idpath. Defined.
Lemma test {A} {x y : A} {p q : x ~~> y} (R : p ~~> q) :
adjust_l R ~~> adjust_l2 R.
Proof.
induction R; induction x0.
path_via (idpath_left_unit (idpath x) @ idpath (idpath x)).
Qed.
Fascinating! It doesn’t really bother me too much that these “proofs” are “relevant”, because as a homotopy theorist, I don’t call these things “proofs of theorems” but rather “constructions of paths.” And “obviously” when you construct a path, it can matter which path you construct.
(-:But it does seem a little unfortunate that we have to pay attention to details like this.It seems to me that the basic status of proof-irrelevance — the idea that certain types are in some sense “propositions”, and for them one should have proof-irrelevance — hasn’t changed; we’ve simply jettisoned the principle that equality should always be such a proposition.
Indeed, arguably we haven’t even lost that much! It’s quite consistent that there’s a “π_{-1}” construction, reflecting types into homotopy-propositions, which are (at least propositionally) proof-irrelevant; and then this applied to the identity type gives a homotopy-proposition representing equality — so, a proof-irrelevant equality. What this lacks compared to full identity types is that one can only eliminate out of it into other homotopy-propositions, not into arbitrary types.