Some months ago I gave a series of hands-on lectures on cubicaltt at Inria Sophia Antipolis that can be found at:
https://github.com/mortberg/cubicaltt/tree/master/lectures
The lectures cover the main features of the system and don’t assume any prior knowledge of Homotopy Type Theory or Univalent Foundations. Only basic familiarity with type theory and proof assistants based on type theory is assumed. The lectures are in the form of cubicaltt files and can be loaded in the cubicaltt proof assistant.
cubicaltt is based on a novel type theory called Cubical Type Theory that provides new ways to reason about equality. Most notably it makes various extensionality principles, like function extensionality and Voevodsky’s univalence axiom, into theorems instead of axioms. This is done such that these principles have computational content and in particular that we can transport structures between equivalent types and that these transports compute. This is different from when one postulates the univalence axiom in a proof assistant like Coq or Agda. If one just adds an axiom there is no way for Coq or Agda to know how it should compute and one looses the good computational properties of type theory. In particular canonicity no longer holds and one can produce terms that are stuck (e.g. booleans that are neither true nor false but don’t reduce further). In other words this is like having a programming language in which one doesn’t know how to run the programs. So cubicaltt provides an operational semantics for Homotopy Type Theory and Univalent Foundations by giving a computational justification for the univalence axiom and (some) higher inductive types.
Cubical Type Theory has a model in cubical sets with lots of structure (symmetries, connections, diagonals) and is hence consistent. Furthermore, Simon Huber has proved that Cubical Type Theory satisfies canonicity for natural numbers which gives a syntactic proof of consistency. Many of the features of the type theory are very inspired by the model, but for more syntactically minded people I believe that it is definitely possible to use cubicaltt without knowing anything about the model. The lecture notes are hence written with almost no references to the model.
The cubicaltt system is based on Mini-TT:
"A simple type-theoretic language: Mini-TT" (2009) Thierry Coquand, Yoshiki Kinoshita, Bengt Nordström and Makoto Takeya In "From Semantics to Computer Science; Essays in Honour of Gilles Kahn"
Mini-TT is a variant Martin-Löf type theory with datatypes and cubicaltt extends Mini-TT with:
- Path types
- Compositions
- Glue types
- Id types
- Some higher inductive types
The lectures cover the first 3 of these and hence correspond to sections 2-7 of:
"Cubical Type Theory: a constructive interpretation of the univalence axiom" Cyril Cohen, Thierry Coquand, Simon Huber and Anders Mörtberg To appear in post-proceedings of TYPES 2016 https://arxiv.org/abs/1611.02108
I should say that cubicaltt is mainly meant to be a prototype implementation of Cubical Type Theory in which we can do experiments, however it was never our goal to implement a competitor to any of the more established proof assistants. Because of this there are no implicit arguments, type classes, proper universe management, termination checker, etc… Proofs in cubicaltt hence tend to get quite verbose, but it is definitely possible to do some fun things. See for example:
- binnat.ctt – Binary natural numbers and isomorphism to unary numbers. Example of data and program refinement by doing a proof for unary numbers by computation with binary numbers.
- setquot.ctt – Formalization of impredicative set quotients á la Voevodsky.
- hz.ctt –
defined as an (impredicative set) quotient of
nat * nat. - category.ctt – Categories. Structure identity principle. Pullbacks. (Due to Rafaël Bocquet)
- csystem.ctt – Definition of C-systems and universe categories. Construction of a C-system from a universe category. (Due to Rafaël Bocquet)
For a complete list of all the examples see:
https://github.com/mortberg/cubicaltt/tree/master/examples
For those who cannot live without implicit arguments and other features of modern proof assistants there is now an experimental cubical mode shipped with the master branch of Agda. For installation instructions and examples see:
https://agda.readthedocs.io/en/latest/language/cubical.html
https://github.com/Saizan/cubical-demo
In this post I will give some examples of the main features of cubicaltt, but for a more comprehensive introduction see the lecture notes. As cubicaltt is an experimental prototype things can (and probably will) change in the future (e.g. see the paragraph on HITs below).
The basic type theory
The basic type theory on which cubicaltt is based has Π and ∑ types (with eta and surjective pairing), a universe U, datatypes, recursive definitions and mutually recursive definitions (in particular inductive-recursive definitions). Note that general datatypes and (mutually recursive) definitions are not part of the version of Cubical Type Theory in the paper.
Below is an example of how natural numbers and addition are defined:
data nat = zero
| suc (n : nat)
add (m : nat) : nat -> nat = split
zero -> m
suc n -> suc (add m n)
If one loads this in the cubicaltt read-eval-print-loop one can compute things:
> add (suc zero) (suc zero) EVAL: suc (suc zero)
Path types
The homotopical interpretation of equality tells us that we can think of an equality proof between a and b in a type A as a path between a and b in a space A. cubicaltt takes this literally and adds a primitive Path type that should be thought of as a function out of an abstract interval with fixed endpoints.
We call the elements of the interval names/directions/dimensions and typically use i, j, k to denote them. The elements of the interval
are generated by the following grammar (where dim is a dimension like i, j, k…):
r,s := 0
| 1
| dim
| - r
| r /\ s
| r \/ s
The endpoints are 0 and 1, – corresponds to symmetry (r in is mapped to
1-r), while /\ and \/ are so called “connections”. The connections can be thought of mapping r and s in to
min(r,s) and max(r,s) respectively. As Path types behave like functions out of the interval there is both path abstraction and application (just like for function types). Reflexivity is written:
refl (A : U) (a : A) : Path A a a = <i> a
and corresponds to a constant path:
<i> a
a -----------> a
with the intuition is that <i> a is a function \(i : . However for deep reasons the interval isn’t a type (as it isn’t fibrant) so we cannot write functions out of it directly and hence we have this special notation for path abstraction.) -> a
If we have a path from a to b then we can compute its left end-point by applying it to 0:
face0 (A : U) (a b : A) (p : Path A a b) : A = p @ 0
This is of course convertible to a. We can also reverse a path by using symmetry:
sym (A : U) (a b : A) (p : Path A a b) : Path A b a = <i> p @ -i
Assuming that some arguments could be made implicit this satisfies the equality
sym (sym p) == p
judgmentally. This is one of many examples of equalities that hold judgmentally in cubicaltt but not in standard type theory where sym would be defined by induction on p. This is useful for formalizing mathematics, for example we get the judgmental equality C^op^op == C for a category C that cannot be obtained in standard type theory with the usual definition of category without using any tricks (see opposite.ctt for a formal proof of this).
We can also directly define cong (or ap or mapOnPath):
cong (A B : U) (f : A -> B) (a b : A) (p : Path A a b) :
Path B (f a) (f b) = <i> f (p @ i)
Once again this satisfies some equations judgmentally that we don’t get in standard type theory where this would have been defined by induction on p:
cong id p == p cong g (cong f p) == cong (g o f) p
Finally the connections can be used to construct higher dimensional cubes from lower dimensional ones (e.g. squares from lines). If p : Path A a b then <i j> p @ i /\ j is the interior of the square:
p
a -----------------> b
^ ^
| |
| |
<j> a | | p
| |
| |
| |
a -----------------> a
<i> a
Here i corresponds to the left-to-right dimension and j corresponds to the down-to-up dimension. To compute the left and right sides just plug in i=0 and i=1 in the term inside the square:
<j> p @ 0 /\ j = <j> p @ 0 = <j> a (p is a path from a to b) <j> p @ 1 /\ j = <j> p @ j = p (using eta for Path types)
These give a short proof of contractibility of singletons (i.e. that the type (x : A) * Path A a x is contractible for all a : A), for details see the lecture notes or the paper. Because connections allow us to build higher dimensional cubes from lower dimensional ones they are extremely useful for reasoning about higher dimensional equality proofs.
Another cool thing with Path types is that they allow us to give a direct proof of function extensionality by just swapping the path and lambda abstractions:
funExt (A B : U) (f g : A -> B)
(p : (x : A) -> Path B (f x) (g x)) :
Path (A -> B) f g = <i> \(a : A) -> (p a) @ i
To see that this makes sense we can compute the end-points:
(<i> \(a : A) -> (p a) @ i) @ 0 = \(a : A) -> (p a) @ 0= \(a : A) -> f a= f
and similarly for the right end-point. Note that the last equality follows from eta for Π types.
We have now seen that Path types allows us to define the constants of HoTT (like cong or funExt), but when doing proofs with Path types one rarely uses these constants explicitly. Instead one can directly prove things with the Path type primitives, for example the proof of function extensionality for dependent functions is exactly the same as the one for non-dependent functions above.
We cannot yet prove the principle of path induction (or J) with what we have seen so far. In order to do this we need to be able to turn any path between types A and B into a function from A to B, in other words we need to be able to define transport (or cast or coe):
transport : Path U A B -> A -> B
Composition, filling and transport
The computation rules for the transport operation in cubicaltt is introduced by recursion on the type one is transporting in. This is quite different from traditional type theory where the identity type is introduced as an inductive family with one constructor (refl). A difficulty with this approach is that in order to be able to define transport in a Path type we need to keep track of the end-points of the Path type we are transporting in. To solve this we introduce a more general operation called composition.
Composition can be used to define the composition of paths (hence the name). Given paths p : Path A a b and q : Path A b c the composite is obtained by computing the missing top line of this open square:
a c
^ ^
| |
| |
<j> a | | q
| |
| |
| |
a ----------------> b
p @ i
In the drawing I’m assuming that we have a direction i : in context that goes left-to-right and that the j goes down-to-up (but it’s not in context, rather it’s implicitly bound by the comp operation). As we are constructing a Path from a to c we can use the i and put p @ i as bottom. The code for this is as follows:
compPath (A : U) (a b c : A)
(p : Path A a b) (q : Path A b c) : Path A a c =
<i> comp (<_> A) (p @ i)
[ (i = 0) -> <j> a
, (i = 1) -> q ]
One way to summarize what compositions gives us is the so called “box principle” that says that “any open box has a lid”. Here “box” means (n+1)-dimensional cube and the lid is an n-dimensional cube. The comp operation takes as second argument the bottom of the box and then a list of sides. Note that the collection of sides doesn’t have to be exhaustive (as opposed to the original cubical set model) and one way to think about the sides is as a collection of constraints that the resulting lid has to satisfy. The first argument of comp is a path between types, in the above example this path is constant but it doesn’t have to be. This is what allows us to define transport:
transport (A B : U) (p : Path U A B) (a : A) : B = comp p a []
Combining this with the contractibility of singletons we can easily prove the elimination principle for Path types. However the computation rule does not hold judgmentally. This is often not too much of a problem in practice as the Path types satisfy various judgmental equalities that normal Id types don’t. Also, having the possibility to reason about higher equalities directly using path types and compositions is often very convenient and leads to very nice and new ways to construct proofs about higher equalities in a geometric way by directly reasoning about higher dimensional cubes.
The composition operations are related to the filling operations (as in Kan simplicial sets) in the sense that the filling operations takes an open box and computes a filler with the composition as one of its faces. One of the great things about cubical sets with connections is that we can reduce the filling of an open box to its composition. This is a difference compared to the original cubical set model and it provides a significant simplification as we only have to explain how to do compositions in open boxes and not also how to fill them.
Glue types and univalence
The final main ingredient of cubicaltt are the Glue types. These are what allows us to have a direct algorithm for composition in the universe and to prove the univalence axiom. These types add the possibility to glue types along equivalences (i.e. maps with contractible fibers) onto another type. In particular this allows us to directly define one of the key ingredients of the univalence axiom:
ua (A B : U) (e : equiv A B) : Path U A B =
<i> Glue B [ (i = 0) -> (A,e)
, (i = 1) -> (B,idEquiv B) ]
This corresponds to the missing line at the top of:
A B
| |
e | | idEquiv B
| |
V V
B --------> B
B
The sides of this square are equivalences while the bottom and top are lines in direction i (so this produces a path from A to B as desired).
We have formalized three proofs of the univalence axiom in cubicaltt:
- A very direct proof due to Simon Huber and me using higher dimensional glueing.
- The more conceptual proof from section 7.2 of the paper in which we show that the
ungluefunction is an equivalence (formalized by Fabian Ruch). - A proof from
uaand its computation rule (uabeta). Both of these constants are easy to define and are sufficient for the full univalence axiom as noted in a post by Dan Licata on the HoTT google group.
All of these proofs can be found in the file univalence.ctt and are explained in the paper (proofs 1 and 3 are in Appendix B).
Note that one often doesn’t need full univalence to do interesting things. So just like for Path types it’s often easier to just use the Glue primitives directly instead of invoking the full univalence axiom. For instance if we have proved that negation is an involution for bool we can directly get a non-trivial path from bool to bool using ua (which is just a Glue):
notEq : Path U bool bool = ua boob bool notEquiv
And we can use this non-trivial equality to transport true and compute the result:
> transport notEq true EVAL: false
This is all that the lectures cover, in the rest of this post I will discuss the two extensions of cubicaltt from the paper and their status in cubicaltt.
Identity types and higher inductive types
As pointed out above the computation rule for Path types doesn’t hold judgmentally. Luckily there is a neat trick due to Andrew Swan that allows us to define a new type that is equivalent to Path A a b for which the computation rule holds judgmentally. For details see section 9.1 of the paper. We call this type Id A a b as it corresponds to Martin-Löf’s identity type. We have implemented this in cubicaltt and proved the univalence axiom expressed exclusively using Id types, for details see idtypes.ctt.
For practical formalizations it is probably often more convenient to use the Path types directly as they have the nice primitives discussed above, but the fact that we can define Id types is very important from a theoretical point of view as it shows that cubicaltt with Id is really an extension of Martin-Löf type theory. Furthermore as we can prove univalence expressed using Id types we get that any proof in univalent type theory (MLTT extended with the univalence axiom) can be translated into cubicaltt.
The second extension to cubicaltt are HITs. We have a general syntax for adding these and some of them work fine on the master branch, see for example:
- circle.ctt – The circle as a HIT. Computation of winding numbers.
- helix.ctt – The loop space of the circle is equal to Z.
- susp.ctt – Suspension and n-spheres.
- torsor.ctt – Torsors. Proof that S1 is equal to BZ, the classifying
space of Z. (Due to Rafaël Bocquet) - torus.ctt – Proof that Torus = S1 * S1 in only 100 loc (due to Dan
Licata).
However there are various known issues with how the composition operations compute for recursive HITs (e.g. truncations) and HITs where the end-points contain function applications (e.g. pushouts). We have a very experimental branch that tries to resolve these issues called “hcomptrans”. This branch contains some new (currently undocumented) primitives that we are experimenting with and so far it seems like these are solving the various issues for the above two classes of more complicated HITs that don’t work on the master branch. So hopefully there will soon be a new cubical type theory with support for a large class of HITs.
That’s all I wanted to say about cubicaltt in this post. If someone plays around with the system and proves something cool don’t hesitate to file a pull request or file issues if you find some bugs.
Thanks for this very nice introduction! It’s exciting that we have cubicaltt to experiment with.
I find it interesting that you say that connections make things simpler; I would rather do without them if I could. The connections introduce lots of judgmental equalities (the axioms of a de Morgan algebra) that don’t feel “computational” to me — in particular, they’re not “directed” — whereas box-filling is an operation that could be computed. It seems that the only real reason that connections are needed is to make singletons contractible, and the algebraic theory of a de Morgan algebra seems like a lot of complicated judgmental machinery in order to achieve that simple result. Is there a theoretical obstacle to doing cubical type theory without connections, or is it just a choice that could be made either way?
I also find it conceptually unsatisfying that function extensionality arises by simple rearranging of lambdas — and hence holds “judgmentally” in some sense — whereas univalence requires postulating these new “Glue” types. I wish there were some way to make univalence hold judgmentally too, but I haven’t been able to think of any such, and I presume no one else has either. Would it at least be possible to replace the Glue types with operations that literally say “every equivalence gives rise to a path in the universe” and so on, rather than transporting an existing path along an equivalence?
Thank you Mike! I was hoping someone would ask about the connections. In the beginning when we switched to cubical sets with connections I also felt like they were quite complicated. But the key point is that they allow us to reduce filling to composition which is a huge simplification for the model as we now only have to define the algorithm for composition and get filling for free. In the BCH cubical set model this is not the case and for Pi one has to first define composition and then filling (see Thm. 6.2 in the BCH paper). The same goes for the symmetries, without them we have to explain how to do comp/fill both up and down. The algorithms are of course the same up to symmetry, but without symmetries we need to give both of them. So it seems to me like the more structure you have in the base site the simpler the comp/fill structures become for your cubical sets. As comp/fill are the most subtle part of the system I think you really want to have them as simple as possible if you want to construct a type theory from the model.
I should also say that for formalization in cubicaltt the connections are very useful. Once one get used to them they are quite ubiquitous, especially when doing higher dimensional compositions. I have a hard time imagining using a cubical type theory without them these days. One could of course do the proofs like in traditional type theory using only J, but as we don’t have the computation rule for J judgmentally this is not very nice. Also it is not very fun to do the same old proofs in cubicaltt, it is much more fun to do things with the new primitives cubicaltt gives us (I tried to illustrate this in some of the exercises in the lecture notes). I also feel like that there must be some examples of where the proof using J is very long and complicated, but where the proof using comp and connections is a lot simpler.
I’ll say something about Glue types in another comment later.
I’m allergic to any mention of “constructing a type theory from the (i.e.from one specific) model”. (-: In my view, a respectable type theory should have models in a general class of categories. This is one of the things that makes me most suspicious of cubical type theory, and hesitant to use it for any substantial synthetic homotopy theory. We understand (modulo initiality theorems and strictness of the universe) how traditional MLTT has semantics in any nice simplicial model category, in particular including models for any locally cartesian closed locally presentable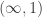 -category. But such a result still seems to be lacking for cubical type theories, and it seems to me that the strict de Morgan algebra structure of the connections would make it harder. If we left them out, we could in principle interpret the cubical interval as an arbitrary interval object (although we’d still have to deal with uniformity).
-category. But such a result still seems to be lacking for cubical type theories, and it seems to me that the strict de Morgan algebra structure of the connections would make it harder. If we left them out, we could in principle interpret the cubical interval as an arbitrary interval object (although we’d still have to deal with uniformity).
I’m allergic to type theories that don’t enjoy canonicity. In my view, a respectable type theory shouldn’t have any axioms. 🙂 More seriously though, I haven’t been thinking much about more general classes of models for cubicaltt yet, but as you probably know there is some work in this direction (Orton & Pitts, Sattler, Guarded CTT…). But as far as I know the connections seem necessary in order to give a reasonably simple operational semantics for comp/fill when formulated the way we do things. There is also the computational higher-dimensional type theory of Angiuli, Harper and Wilson that uses a different notion of composition structure where filling can be reduced to comp without connections, but as far as I know they haven’t gotten the universe to work yet… Designing cubical type theories is a bit like chemistry, there are a lot of things you can throw in the mix but if you don’t get things right the experiment doesn’t work out (or it blows up in your face).
I guess one could imagine designing a version of cubicaltt without connections. The main drawback for the formulation of the type theory would be that we have to do twice as much work for some type formers (I guess as least for Pi and Glue) as we have to define first the equality judgment for comp and then fill. But it could maybe work out. However as I said in my previous message the connections are very useful for practical formalization. I rarely formalize any statement without at least one connection in it when working in cubicaltt, so removing them would make working in the type theory a lot less convenient and fun. So maybe one should first figure out if it’s possible or not to interpret cubicaltt in the classes of models you are interested in before throwing out the connections.
I do appreciate the importance of canonicity! I have faith that it’s possible to design a type theory that both of us would consider respectable. I certainly see that from an implementation perspective, it would be more work to define how fill computes than to include connections; but conceptually I think I would find it simpler, since the computation laws feel “secondary” relative to the specification of the terms (even though formally, in dependent type theory all the judgments are bound up in one big mutual induction).
Can you point to some good examples of where you’ve found connections useful in formalization?
Here comes two simple examples of where connections are useful:
First let’s say we want to define the integers as a HIT with two constructors
posandnegboth taking anatand a pathzeroP : pos 0 = neg 0. It is easy to define functions back and forth to the non-HIT definitions of Z (defined asnat + nat), but when we need to prove that these are inverse we end up having to construct a path in direction i from<j> pos 0tozeroP. This is easily done with a connection:<j> zeroP @ i /\ j. At i=0 we have<j> pos 0and at i=1 we havezeroP. For details see:https://github.com/mortberg/cubicaltt/blob/master/examples/integer.ctt#L57
Another example is when one defines the multiplication operation on S1 as part of the Hopf fibration. There one ends up building a square with loop on all its sides (in the latest version of the HoTT book this is part of lemma 6.4.2 where one instead proves that “loop^-1 . loop . loop = loop”). In cubicaltt such a constant square cannot be built directly using connections, instead we need to use a composition where the sides are built using connections:
https://github.com/mortberg/cubicaltt/blob/master/examples/prelude.ctt#L152
The definition of mult is then direct:
https://github.com/mortberg/cubicaltt/blob/master/examples/circle.ctt#L47
It takes some getting used to to come up with this kind of proofs, but the idea is that if we have “p : Path A a b” then we can build the following six squares (the other two are symmetric to two of them) directly using connections:
These correspond to the following equations:
These should be read as representing squares with the LHS as the left and upper side, and similar for the RHS. If you’re lucky the square you are trying to construct is one of these basic ones (like in the integer example above) and you are done. Otherwise you have to use a composition as in the case of the constant square. In higher dimensions it is of course harder to draw things, but it is still possible to do things. With proper IDE support I think this kind of proofs could be made interactively, but at the moment you have to find the whole composition by hand on paper and then write it up in cubicaltt. Also, constructing these higher cubes is a purely combinatorial problem and I imagine that one could come up with a clever algorithm that finds the solution.
I see; by making squares and cubes “basic things” rather than defining them in terms of composition, we lose the ability to construct a lot of “obvious” ones easily. I could see getting used to connections (in fact one might be surprised at my resistance to them, given how much I like double categories). But I really want to see the semantic question settled.
I’m glad that you’re a little less resistant to connections now! They are really useful and if you look at some of the .ctt files you will see them everywhere. When I do proofs in cubicaltt these days I almost never use J, and if I do I feel like I just haven’t come up with a clever composition with the right connections yet.
I’ve been thinking some more about the semantic question the last few days, I don’t have anything interesting mathematically to say but I find it interesting that you have this criteria for “respectable type theories”. To me models are mainly useful for two things: First of all to establish that your theory is consistent. In the case of cubicaltt we constructed the type theory from the model so it is not too surprising that we can intepret it in the model (however this was a lot more subtle than I expected!). Second, to prove independence results, e.g. that UIP is independent of MLTT as established by the groupoid model. However you seem to have a third application in mind. I guess if the theory is interpretable into a general class of categories then anything we say in the type theory means something in these categories? I understand why this could be important if you are usually working with this kind of categories, but why should this be important to me as a type theorist? In particular, is this useful/important for something else than synthetic homotopy theory? (I’m becoming more interested in these questions now, the reason I haven’t been thinking about more general classes of models so far is simply because I haven’t understood why I should be thinking about them)
Thierry presented a bit of progress on (cubical) stack models [here](https://hott-uf.github.io/2017/slides/Coquand.pdf).
About Glue types: I think it is interesting that function extensionality has this very simple proof while univalence is very complicated. Maybe one hint at why this is the case comes from looking at the attempts to make an OTT style theory higher dimensional (i.e. define HOTT 🙂 ). In OTT the equality judgments are defined by induction on the type (just like in cubicaltt). For Pi types the equality is defined to be extensional (in the sense of function extensionality) and this is not too complicated, however when trying to make the equality for the universe into something like univalence in the non-truncated theory one seem to end up with a combinatorial explosion. As far as I know noone has figured out a way to do this yet.
The Glue types are used for 2 things in cubicaltt:
1. Prove univalence
2. Define composition for U
Is it clear that we can do 2 from what you suggest? If not we would have to define this separately which is about as complicated as composition for Glue…
In principle I find it clear that it should be possible. For instance, consider composition of a 1-box in U with sides p,q,r. In CCHM cubical type theory, we do this by making the paths p and r into equivalences and using a Glue type to transport q along these equivalences. In my proposal, we would do it by making all three of p,q,r into equivalences, composing these equivalences as equivalences, and then making the result back into a path. Higher composition is, I agree, much more combinatorially complicated: for instance, a square in U corresponds to a homotopy between the top-right and bottom-left composites of equivalences, and to compose a 2-box in U we need to compose five of these homotopies whiskered in appropriate ways. But in principle it should be possible, because there is an -groupoid whose objects are
-groupoid whose objects are  -groupoids, whose morphisms are equivalences, whose 2-morphisms are homotopies, etc. Making this precise is basically the problem of relating globular and cubical notions of
-groupoids, whose morphisms are equivalences, whose 2-morphisms are homotopies, etc. Making this precise is basically the problem of relating globular and cubical notions of  -groupoid explicitly and algebraically, which is hard but should be possible. (-:
-groupoid explicitly and algebraically, which is hard but should be possible. (-:
Here is another reason that I dislike connections. One of the things I like so much about Book HoTT is how we don’t have to stipulate that types are -groupoids; we just decline to assert UIP, and all the structure of an
-groupoids; we just decline to assert UIP, and all the structure of an  -groupoid emerges automatically from J. I find this philosophically very appealing: it means that the notion of
-groupoid emerges automatically from J. I find this philosophically very appealing: it means that the notion of  -groupoid is implicit in the very notion of “equality”.
-groupoid is implicit in the very notion of “equality”.
At first glance, cubical type theory destroys all this, since it builds all the higher-dimensional structure of an -groupoid into the composition operations. But there is a different way of looking at cubical type theory that retains some of the pleasing philosophy; I’m not sure who first explained this to me, but I’ve only recently come to really appreciate it.
-groupoid into the composition operations. But there is a different way of looking at cubical type theory that retains some of the pleasing philosophy; I’m not sure who first explained this to me, but I’ve only recently come to really appreciate it.
In Book HoTT, operations such as transport and path composition are defined by induction on the paths; thus they reduce when the paths are reflexivity, but are stuck otherwise. However, we can prove (as in Chapter 2) that they also reduce typally (i.e. up to an identification rather than a judgmental equality) based on the form of the type we are composing in or transporting along. Moreover, experience suggests that these “reductions” are used more often than the reduction on reflexivity paths, so it’s natural to “change the rules” to make the type-based reductions judgmental instead of the path-based ones.
On the surface this doesn’t seem to require anything higher-dimensional, but it turns out to give rise to box filling filling/composition in all dimensions because of path-types: transport in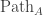 reduces to 1-box filling in
reduces to 1-box filling in  , 1-box filling in
, 1-box filling in 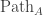 reduces to 2-box filling in
reduces to 2-box filling in  , and so on. So once again the
, and so on. So once again the  -groupoid structure “arises automatically” rather than being “put in by hand because we want types to be
-groupoid structure “arises automatically” rather than being “put in by hand because we want types to be  -groupoids”; the only difference is that this “arising” happens at the level of the design of the type theory rather than when working inside an already extant theory.
-groupoids”; the only difference is that this “arising” happens at the level of the design of the type theory rather than when working inside an already extant theory.
However, while it’s quite easy to explain/motivate box-filling in addition to mere composition this way, I have a harder time thinking of how to motivate connections.
In the *cartesian* cubical sets (i.e. w/o connections), the Kan objects do have connections, in the sense that there are always maps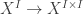 (satisfying the expected equations), they just don’t come from representable maps
(satisfying the expected equations), they just don’t come from representable maps  . Instead, they comes from filling certain boxes. So the Kan objects support many of the same constructions involving connections as in the lattice-based cubical sets, except of course one cannot reduce filling to composition. We have found that this serves many of the purposes for which connections are used in other work — *except* that the cubes themselves lack connections, even in this sense, since they are not Kan.
. Instead, they comes from filling certain boxes. So the Kan objects support many of the same constructions involving connections as in the lattice-based cubical sets, except of course one cannot reduce filling to composition. We have found that this serves many of the purposes for which connections are used in other work — *except* that the cubes themselves lack connections, even in this sense, since they are not Kan.
Is there a good reason to prefer (power-sets and lattice maps) over (power-sets and monotone maps)?
I think the cartesian cubes seem very nice, but what is the status for the universe? Do you have a constructive proof that it is Kan?
not yet!
I thought I remembered this, but then I wasn’t able to reproduce the argument myself so I didn’t mention it. (Where) is it written down?
It’s lemma 29 in this paper:
Click to access 1607.06413.pdf
although the proof is not given there, so here it is: , we have a map
, we have a map 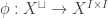 that chooses fillers for open 2-boxes. Let
that chooses fillers for open 2-boxes. Let  be the map that takes a path
be the map that takes a path 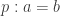 in
in  to the evident open box with sides
to the evident open box with sides 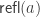 and
and  (say, pointing “up”) and base
(say, pointing “up”) and base  . Then an (upper) connection is the composite
. Then an (upper) connection is the composite  . The lower one is obtained by filling “down” rather than “up”. These connections are not in general strict, in the sense that the resulting fourth side need not be
. The lower one is obtained by filling “down” rather than “up”. These connections are not in general strict, in the sense that the resulting fourth side need not be  . One can also define connections for the filling problem in which two sides are
. One can also define connections for the filling problem in which two sides are  and one is
and one is 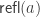 , but then the fourth side need not be a
, but then the fourth side need not be a  . However, such strictness is not required for the algebraic weak factorization system, or for the
. However, such strictness is not required for the algebraic weak factorization system, or for the 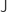 computation rule with
computation rule with  , as shown in the paper.
, as shown in the paper.
By uniform box filling for
Ah, I had certainly come up with that much argument, but then I got stuck because I was expecting to get a strict connection. Some of the applications of connections that Anders mentioned certainly do need (at least apparently) the connections to be strict, e.g. the square in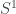 with boundary
with boundary  . Can you at least show that the fourth side is homotopic to
. Can you at least show that the fourth side is homotopic to  ?
?
Intuitively, it seems to me that for a sensible theory of “cubical -groupoids”, it ought to be the case that a square with sides
-groupoids”, it ought to be the case that a square with sides  (in appropriate order) should be the same as a homotopy from
(in appropriate order) should be the same as a homotopy from 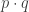 to
to  . But if this were true, then since
. But if this were true, then since 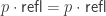 , we would be able to use it to construct a strict connection. So are you saying that this equivalence between squares and homotopies isn’t true for cartesian cubical sets?
, we would be able to use it to construct a strict connection. So are you saying that this equivalence between squares and homotopies isn’t true for cartesian cubical sets?
I don’t know, but this is certainly a reasonable thought. I tried for a few minutes (to put together a higher-dimensional filling problem) and didn’t see how to do it, but it would be nice if it could be done!
What would be the obstacles to automatically translating cubical code to cubical agda?
I guess the main obstacle is that cubical Agda doesn’t have much support for HITs yet. But for code that doesn’t involve HITs I don’t see any deep reasons why there would be a problem. One might of course have to be a bit more careful about things like universe levels (cubicaltt has U:U…) and I guess one also would want to be clever in order to remove information that can be implicit so that the resulting Agda code looks nicer.
How do you ask Agda to evaluate or normalize something the way you can at the cubicaltt prompt?
I haven’t used Agda for years, but I seem to recall that one can do C-c C-n and then type the thing you want to have Agda normalize?
How important is it in practice that the connections satisfy the de Morgan algebra axioms? Of course we need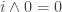 ,
,  , and so on so that the connection squares have the correct boundaries. But do we really need
, and so on so that the connection squares have the correct boundaries. But do we really need  and
and 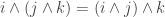 and
and 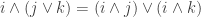 , etc.?
, etc.?
I don’t think it’s too important and that we can do with something a lot weaker. See the “connection algebra structure” in Figure 1 of https://www.repository.cam.ac.uk/handle/1810/260785
Thanks for the pointer. It looks like a “connection algebra structure” is exactly the laws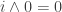 and so on. If that’s all we need to assume about the operations
and so on. If that’s all we need to assume about the operations 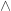 and
and  , it makes me significantly happier.
, it makes me significantly happier.
Good! If I remember correctly Orton & Pitts do everything up to the universe, but as they are working in a general topos they cannot construct a universe. However if you are in a presheaf topos the usual universe construction should work and I would be very surprised if you need any more structure on the connections to prove that it’s also fibrant (once you have the Glue types you should be done).
(Replying down here to this comment to reduce the comment nesting depth.)
I guess if the theory is interpretable into a general class of categories then anything we say in the type theory means something in these categories?
Yes, exactly; a type theory is a presentation of the initial object in some category of structured categories. I wrote a fairly detailed exposition of this perspective and its applications in The logic of space.
why should this be important to me as a type theorist?
Well, what does it mean to you to “be a type theorist”? Type theory is a lot of things, but one of the things it is is a presentation of the initial object in some category. So it would seem to me that that’s unquestionably something a “type theorist” should be interested in. To me, a type theorist who thinks of categorical semantics as important only for consistency and independence results for syntax is as backwards as a knot theorist who thinks of embeddings of circles in as important only to prove the consistency and independence of the Reidemeister moves.
as important only to prove the consistency and independence of the Reidemeister moves.
Of course my tongue is in my cheek here, but the question is genuine: what do you mean more specifically when you say “as a type theorist”?
I had in mind more syntactically minded type theorists (maybe proof theorists/logicians would have been more accurate) who study the meta-theory of type theories without any categories involved (so proving normalization, decidability of type checking, proof theoretic strength, etc.). From this perspective cubicaltt is a perfectly fine theory (assuming that we can extend Simon’s canonicity proof to a normalization proof), so I was just curious exactly why it was so important for you to also have a general class of models for this to be a “respectable type theory”. Luckily my guess was correct and it’s definitely something I can appreciate! It’s also more clear to me now why all of the extra structure in cubicaltt might affect this negatively: if the term model of cubicaltt is the initial object in some too restrictive category of structured categories there might not be too many interesting categories for it to map to.
A problem with the sort of purely syntactic point of view that you are suggesting, it seems to me, is that it’s then not clear what cubicaltt is a theory *of*. The old MLTT is a (type) theory of propositions, sets, constructions, functions, identity, etc. Cubicaltt is not just that, because it also has all those dimension variables, cubes, composition and gluing operations, and so on. Are these supposed to describe some geometric objects, like spaces, simplicial and cubical sets, or maybe even -groupoids? If so, it seems like there should be some attempt to model it in various *different* settings, but that doesn’t work because of all the specific judgmental equalities. But if there is then just supposed to be the one canonical interpretation, then what the heck is it? Some sort of cubical constructions? What’s that?
-groupoids? If so, it seems like there should be some attempt to model it in various *different* settings, but that doesn’t work because of all the specific judgmental equalities. But if there is then just supposed to be the one canonical interpretation, then what the heck is it? Some sort of cubical constructions? What’s that?
It seems to me this is a type theory made to order with some interesting properties, like canonicity, but it’s not exactly clear what it is supposed to mean — except of course, that it’s close to another theory that does have a clear geometric meaning, namely HoTT.
Thanks for the clarification! I see what you mean and why there might a priori be a problem with all of the extra judgmental equalities. But as far as I understand it it is not yet clear that it isn’t possible to model cubicaltt in different settings and various people are working on this. For instance there is the paper by Orton & Pitts where they show that one can do our model construction with a lot weaker assumptions (in particular one doesn’t need the full de Morgan algebra structure).
To me it’s at least intuitively clear what the things in cubicaltt are supposed to mean geometrically. The path types are just functions out of an interval with fixed end-points modelling paths (so exactly like in classical topology). The fact that the interval carries the structure of a de Morgan algebra is only natural as this is a theory of the unit interval (in fact we should have more judgmental equalities, not fewer, to model the unit interval exactly. The missing equations are for all x and y which intuitively says that the min of x and 1-x is less than or equal to the max of y and 1-y). The compositions allow us to compose these paths in many different ways, and in all dimensions, together with a general form of path lifting. Finally the glue types are the hardest, but intuitively they just allow us to replace some subspaces of a space with equivalent spaces. When we draw this on the board we usually draw a blob (so a space 🙂 ) and then fill in various parts that are the ones that get replaced by equivalent ones. Hopefully one can make these intuitions precise, but to me none of the things we add are really strange from a geometric point of view.
for all x and y which intuitively says that the min of x and 1-x is less than or equal to the max of y and 1-y). The compositions allow us to compose these paths in many different ways, and in all dimensions, together with a general form of path lifting. Finally the glue types are the hardest, but intuitively they just allow us to replace some subspaces of a space with equivalent spaces. When we draw this on the board we usually draw a blob (so a space 🙂 ) and then fill in various parts that are the ones that get replaced by equivalent ones. Hopefully one can make these intuitions precise, but to me none of the things we add are really strange from a geometric point of view.
For whatever it’s worth, from a truly higher-categorical point of view, one arguably shouldn’t think about topological spaces but rather about -groupoids. In particular, this means one shouldn’t rely too much (either intuitively or technically) on *strict* (i.e. up-to-homeomorphism) structure possessed by the topological unit interval, since it is not homotopy-invariant. Specifically, topological spaces don’t have some of the other nice model-categorical properties of simplicial or cubical sets that get used when constructing models of type theory (e.g. in defining glue types), while combinatorial intervals like the simplicial or cartesian-cubical ones don’t have all the properties of the topological one. I’m not saying your geometric intuition is wrong, but that it’s a bit of a mongrel that may look a little suspicious to a higher category theorist.
-groupoids. In particular, this means one shouldn’t rely too much (either intuitively or technically) on *strict* (i.e. up-to-homeomorphism) structure possessed by the topological unit interval, since it is not homotopy-invariant. Specifically, topological spaces don’t have some of the other nice model-categorical properties of simplicial or cubical sets that get used when constructing models of type theory (e.g. in defining glue types), while combinatorial intervals like the simplicial or cartesian-cubical ones don’t have all the properties of the topological one. I’m not saying your geometric intuition is wrong, but that it’s a bit of a mongrel that may look a little suspicious to a higher category theorist.
However, I’m certainly not saying it’s not possible to model cubicaltt in different settings; just that until it’s known that it is possible, I’m wary of depending too much on it.
The goal of cubical type theory was to provide a model of type theory with univalence and propositional truncation in a constructive metatheory.
The intuitions are logical rather than geometrical. It can be seen as a higher dimensional generalization of Gandy’s model of extensional equality for simple type theory, or of Bishop’s explanation of the notion of set. As for the original dependent type theory, all operations are “justified” by computation rules.
The model was intended to be as simple as possible. Connections are added since they correspond to a fundamental law (singletons are contractible). The conversion rules for connections are part of the description of the higher dimensional structure and should not be thought of as computation rules. Without connections, as in the BCH model, it is much harder to describe the filling structure for the universe (as was done by Simon Huber and Georges Gonthier independently). Similarly symmetries were introduced to simplify the model.
One application of these cubical models is to show that univalence does not add any proof theoretical power to dependent type theory. It is also possible to extend this to sheaf models (in the reference given by Bas above) and to show the consistency with continuity principles. It is not clear at this point how this can be achieved starting from the simplicial set model.
Hopefully these models motivated by logical intuitions are complementary to the ones based on geometrical intuitions. A further remark is that, if Voevodsky’s conjecture holds, then any term of type Bool, built using univalence as an axiom, has the same values in all these models.
my question was, what is the *logical* intuition underlying the dimension variables, if they are not to be understood geometrically? what is meant by “higher dimensional structure”, if not something geometrical?
I think you mean proof theorist narrowly. (Model theory is usually considered to be part of logic.)
True, but the classical model theory I know doesn’t involve any categories either (or type theory for that matter). Thinking more about it I think I had in mind people who are doing (set-level) formalization of mathematics and computer science. For this kind of theories cubicaltt seems very good compared to standard type theory or HoTT as it provides various extensionality principles and quotients without giving up on canonicity.
Right, classical model theory of classical first-order logic uses classical set theory as the context for its models. But just as classical model theory is part of classical logic, so the model theory of type theory, which uses categories as the context for its models, should be considered part of the notion of “logic” applicable to type theory.
In my opinion, everyone who uses constructive type theory, even for set-level formalization, ought to be interested in its plethora of models, because it’s one of the big advantages you get from doing mathematics type-theoretically and constructively. That is, once you’ve formalized something once, constructively, you know automatically that it’s true in all models, and hence that it’s true “continuously” and “computably” and “sheaf-ly” and “smoothly” etc. etc. Thinking of a formalization as only saying something about one model (or using a type theory that’s only known to have one model) is certainly not worthless, but fails to take advantage of a much greater potential.
Of course, Mike should that models also allow us to prove (homotopical) canonicity.
I have another question about CCHM cubical type theory, and this seems as good a place as any to ask it. In Simon’s paper about canonicity, he mentions that a “major difficulty” is that the reduction relation doesn’t commute with name substitutions and (at the end of section 2) that this problem arises ultimately from reduction rules whose premise contains a disequality in the face lattice . This seems rather weird, and my question is why it has to be this way? That is, could one set things up slightly differently so that reduction does commute with name substitution?
. This seems rather weird, and my question is why it has to be this way? That is, could one set things up slightly differently so that reduction does commute with name substitution?
On a quick read-through, I see two groups of reduction rules whose premises involve disequalities in . The first is the rules for the
. The first is the rules for the 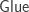 type, where the case
type, where the case  is treated specially and the “ordinary” rules thus have to stipulate
is treated specially and the “ordinary” rules thus have to stipulate  . Is there some reason why
. Is there some reason why  has to be treated specially? It’s obviously true that
has to be treated specially? It’s obviously true that ![\mathsf{Glue}[1\mapsto (T,w)]A](https://s0.wp.com/latex.php?latex=%5Cmathsf%7BGlue%7D%5B1%5Cmapsto+%28T%2Cw%29%5DA&bg=ffffff&fg=333333&s=0&c=20201002) could be defined to reduce to
could be defined to reduce to  , but could we instead just leave
, but could we instead just leave ![\mathsf{Glue}[1\mapsto (T,w)]A](https://s0.wp.com/latex.php?latex=%5Cmathsf%7BGlue%7D%5B1%5Cmapsto+%28T%2Cw%29%5DA&bg=ffffff&fg=333333&s=0&c=20201002) in as a new type (presumably equivalent to
in as a new type (presumably equivalent to  ), and instead apply the “ordinary” reduction rules for
), and instead apply the “ordinary” reduction rules for 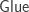 in the case
in the case  ?
?
The second place is the rules for reducing systems, where the condition “ minimal with
minimal with 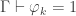 ” involves disequalities
” involves disequalities 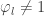 for
for 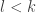 . I think I see why we have to be able to reduce systems to non-systems in order to obtain a canonicity result, since systems aren't among the "canonical forms" we want to get out as answers. However, right now I don't see anywhere that systems are used other than as a way to encode
. I think I see why we have to be able to reduce systems to non-systems in order to obtain a canonicity result, since systems aren't among the "canonical forms" we want to get out as answers. However, right now I don't see anywhere that systems are used other than as a way to encode ![[\varphi_1\mapsto u_1, \dots, \varphi_n\mapsto u_n]](https://s0.wp.com/latex.php?latex=%5B%5Cvarphi_1%5Cmapsto+u_1%2C+%5Cdots%2C+%5Cvarphi_n%5Cmapsto+u_n%5D&bg=ffffff&fg=333333&s=0&c=20201002) as
as ![[\bigvee_l\varphi_l\mapsto [\varphi_1\; u_1,...,\varphi_n\; u_n]]](https://s0.wp.com/latex.php?latex=%5B%5Cbigvee_l%5Cvarphi_l%5Cmapsto+%5B%5Cvarphi_1%5C%3B+u_1%2C...%2C%5Cvarphi_n%5C%3B+u_n%5D%5D&bg=ffffff&fg=333333&s=0&c=20201002) , and it seems to me that in that case the only thing we have to be able to do with systems is build them and compare them for equality. So instead of regarding systems as terms, which therefore have to be reduced, could we instead consider systems as a different syntactic category that can be built from tuples of terms, and compared for equality by dividing into cases based on face restrictions in the context and then comparing their constituent terms? Then maybe we wouldn't need to define reduction of systems at all.
, and it seems to me that in that case the only thing we have to be able to do with systems is build them and compare them for equality. So instead of regarding systems as terms, which therefore have to be reduced, could we instead consider systems as a different syntactic category that can be built from tuples of terms, and compared for equality by dividing into cases based on face restrictions in the context and then comparing their constituent terms? Then maybe we wouldn't need to define reduction of systems at all.
One reason why we need this reduction rule for Glue when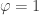 is for example to be able to typecheck:
is for example to be able to typecheck:
ua (A B : U) (e : equiv A B) : Path U A B = <i> Glue B [ (i = 0) -> (A,e) , (i = 1) -> (B,idEquiv B) ]In order to get that the endpoints of this Path really are A and B we must have that Glue reduces when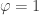 (by the typing rule for Path we will take the (i=0) face of the thing under
(by the typing rule for Path we will take the (i=0) face of the thing under
<i>which will compute toGlue B [ 1 -> (A,e) ]and this has to be convertible with A).I’ll try to think more about the question about systems.
Ah, okay, I see now why that reduction for Glue has to be there. But now let me attack those reductions from a different angle: why do we need the conditions on the reduction rules where it is present? Why couldn’t we also have those rules when
conditions on the reduction rules where it is present? Why couldn’t we also have those rules when 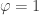 ? It seems to me that their source and target in that case are already judgmentally equal.
? It seems to me that their source and target in that case are already judgmentally equal.
The first one is
If instead of the last premise we have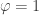 , then
, then ![\mathsf{glue}\, [\varphi\mapsto t] a\succ t](https://s0.wp.com/latex.php?latex=%5Cmathsf%7Bglue%7D%5C%2C+%5B%5Cvarphi%5Cmapsto+t%5D+a%5Csucc+t&bg=ffffff&fg=333333&s=0&c=20201002) by the previous rule, while
by the previous rule, while ![\mathsf{unglue}\, [\varphi\mapsto w] t \succ w.1\, t](https://s0.wp.com/latex.php?latex=%5Cmathsf%7Bunglue%7D%5C%2C+%5B%5Cvarphi%5Cmapsto+w%5D+t+%5Csucc+w.1%5C%2C+t&bg=ffffff&fg=333333&s=0&c=20201002) by the subsequent rule, which is judgmentally equal to
by the subsequent rule, which is judgmentally equal to  (that’s what the notation
(that’s what the notation ![\Gamma\vdash a:A[\varphi\mapsto w.1\,t]](https://s0.wp.com/latex.php?latex=%5CGamma%5Cvdash+a%3AA%5B%5Cvarphi%5Cmapsto+w.1%5C%2Ct%5D&bg=ffffff&fg=333333&s=0&c=20201002) means).
means).
The second rule is
And if instead of the last premise here we have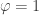 , then
, then ![\mathsf{unglue}\,[\varphi\mapsto w]\,u \succ w.1 u](https://s0.wp.com/latex.php?latex=%5Cmathsf%7Bunglue%7D%5C%2C%5B%5Cvarphi%5Cmapsto+w%5D%5C%2Cu+%5Csucc+w.1+u&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![\mathsf{unglue}\,[\varphi\mapsto w]\,u' \succ w.1 u'](https://s0.wp.com/latex.php?latex=%5Cmathsf%7Bunglue%7D%5C%2C%5B%5Cvarphi%5Cmapsto+w%5D%5C%2Cu%27+%5Csucc+w.1+u%27&bg=ffffff&fg=333333&s=0&c=20201002) , which should be judgmentally equal too.
, which should be judgmentally equal too.
Sorry, I totally forgot to answer to this. I have not studied Simon’s proof very closely, but my intuition why Simon wants this is because he we wants reduction to be deterministic so that only one reduction rule applies at each step (I guess this makes the induction or the logical relations simpler). Simon can surely tell you a lot more about this.
In that Mike has admitted liking connections a bit better, this is coming late, but I wanted to state the thing more fully: connectionful cubical sets are presheaves on (monotone maps of finite powersets), which is a forget-only-structure-extension of finite-boolean-lattices.
I’m not sure what is meant by “forget-only-…”, but the index category of the cubical sets with connections can easily be described as the finite product closure in Cat of the one-arrow category ; that is, all the functors
; that is, all the functors 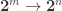 . This differs from the cartesian cubical sets exactly by adding the two connections
. This differs from the cartesian cubical sets exactly by adding the two connections  .
.
An challenging “exercise” is to calculate the size of the Hom-sets in this category, say,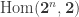 for even small
for even small  .
.
Isn’t the answer the number of elements in a free distributive lattice on 2*n generators (the generators are i and -i)? (so essentially every second Dedekind number. if this is the case I see why it gets really hard after n=4…)
the lattice of order ideals in the poset of subsets of {1,2,3} is not the free distributive lattice on three generators. Very similar, but a bit smaller.
Hmm, I’m not sure if we are talking about the same cubes with connections… There is a jungle of cube categories out there and I’m talking about the one from the paper which this post is based on (so with symmetries and diagonals in addition to connections). This is the cube category in the middle of the down-right corner of Table 2 on page 12 of https://arxiv.org/abs/1701.08189. My understanding is that what Steve refers to as “cartesian cubical sets” is the one based on the cube category on the bottom of column 2 (so with symmetries and diagonals, but no connections)… But maybe we are all talking about different cube categories which would make the exercise even more challenging 🙂
I was asking about the one I described in my comment as the full subcategory of Cat on the finite powers of . This category is dual to that of finitely generated free distributive lattices (by Priestley duality if you like), so the answer is that
. This category is dual to that of finitely generated free distributive lattices (by Priestley duality if you like), so the answer is that 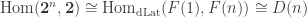 , the
, the  -th Dedekind number (no reversals
-th Dedekind number (no reversals 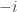 in general distributive lattices).
in general distributive lattices).
By “cartesian cubes” I mean the free finite product category on a bipointed object. By Lawvere duality, this can be described nicely as the dual of finite, strictly bipointed sets with bipointed maps (“strictly” means the points must differ — these are the “free algebras” for this signature).
I see, it looks I’m so used to the reversals that I was thinking of another cube category… So the “cartesian cubes” are the ones at the bottom of the first column of the paper on “Varieties of cubical sets” that I linked before? In their notation these cubes are called C_(wec,.) as they have weakening (i.e. degeneracy maps), exchange (i.e. permutation of dimensions) and contraction (i.e. diagonals), but no reversals and no connections.
we’re still talking about two different categories of cubes, right? The ones with connections (but no reversals) that are dual to distributive lattices, and the “cartesian” ones. The maps in the cartesian category are compositions of faces, degeneracies, symmetries and diagonals. So, in the terminology of that paper, the answer is yes.
[I answer here to reduce nesting]
Oh wait, by “symmetries” you mean the morphisms given by exchange (i.e. permutation of dimensions)? I have been using this synonymously with “reversals” as they allow us to give a direct proof of “symmetry” for path types… I see now that my terminology is maybe confusing and that using symmetries for “exchange” is maybe more natural as it corresponds to rotating/mirroring a cube to obtain an equivalent one up to symmetry (even though “reversal” is a kind of symmetry as well…). I’ll try to update my vocabulary to reduce confusion.
And yes, we are still talking about two cube categories. The “exercise” was for while the cartesian cubes are
while the cartesian cubes are  . (and the answer I gave was for
. (and the answer I gave was for  )
)
OK, nifty, although… I’m having difficulty finding a free reference for “cartesian cubical set”, and whether it means more or less than “cubical set”. Also, “easily described” and “easily seen to be equivalent” are Different Things, which was why I wrote a little note… and still would like to know where/when it was written up before. It’s the sort of thing that shouldn’t stay secret!
One reference for cartesian cubical sets is my paper https://arxiv.org/abs/1607.06413. The unqualified term “cubical set” is now hopelessly ambiguous, I’m afraid.
Now we are getting somewhere!
Is the comp of the constant path along two constant path (i.e. filling the ⊔ shape, with each side a path of the form a) equal to the constant path?
I was trying to do something like
test (A : U) (a : A) :
Path (Path A a a) ( a)
( comp ( A) a
[ (i = 0) -> a,
(i = 1) -> a])
= ( a)
but type checking failed.
I meant
test (A : U) (a : A) :
Path (Path A a a) (‹_› a)
(‹i› comp (‹_› A) a
[ (i = 0) -> ‹_› a,
(i = 1) -> ‹_› a])
= ‹i› (‹_› a)
WordPress comment take ‹i› as HTML tag, so I have to use a weird one.
This is not provable by refl, instead you have to prove it as a more complicated comp. We tried to have a version of cubicaltt where this would be provable by refl but we never got it to work for the case when A is the universe.
Does anybody plan on implementing this interesting theory in Coq?
I don’t know of any project to implement this in Coq, but there is a cubical version of Agda by Andrea Vezzosi that is super cool:
https://agda.readthedocs.io/en/latest/language/cubical.html
https://github.com/Saizan/cubical-demo
Pingback: Cubical Agda | Homotopy Type Theory