As defined in chapter 7 of the book, a modality is an operation on types that behaves somewhat like the n-truncation. Specifically, it consists of a collection of types, called the modal ones, together with a way to turn any type into a modal one
, with a universal property making the modal types a reflective subcategory (or more precisely, sub-(∞,1)-category) of the category of all types. Moreover, the modal types are assumed to be closed under Σs (closure under some other type formers like Π is automatic).
We called them “modalities” because under propositions-as-(some)-types, they look like the classical notion of a modal operator in logic: a unary operation on propositions. Since these are “monadic” modalities — in particular, we have rather than the other way around — they are most closely analogous to the “possibility” modality of classical modal logic. But since they act on all types, not just mere-propositions, for emphasis we might call them higher modalities.
The example of n-truncation shows that there are interesting new modalities in a homotopy world; some other examples are mentioned in the exercises of chapter 7. Moreover, most of the basic theory of n-truncation — essentially, any aspect of it that involves only one value of n — is actually true for any modality.
Over the last year, I’ve implemented this basic theory of modalities in the HoTT Coq library. In the process, I found one minor error in the book, and learned a lot about modalities and about Coq. For instance, my post about universal properties grew out of looking for the best way to define modalities.
In this post, I want to talk about something else I learned about while formalizing modalities: Coq’s modules, and in particular their universe-polymorphic nature. (This post is somewhat overdue in that everything I’ll be talking about has been implemented for several months; I just haven’t had time to blog about it until now.)
It took me a long time to get any idea of what Coq’s modules are and what they are for. I didn’t find the documentation in the Coq reference manual to be very helpful: it seems to be written for a reader who already knows what modules are and only wants to know the appropriate syntax to use them in Coq. The general idea of modules seems to be inherited from ML; but in ML modules seem mainly to be used for things that in Coq I would be inclined to use dependent records or typeclasses for, like defining “a group” to be a type together with appropriate operations and axioms. So why, I wondered, does Coq have modules at all?
One reason is for namespacing. Unlike a record, a module can be “imported”, so that all of its fields can be accessed without having to mention the module’s name all the time. In fact, every file in Coq is implicitly its own module, and when you say Require Import Filename. you are actually importing a module. Similarly, modules are used for access control in Dan Licata’s private-inductive-types hack that we use to define HITs that compute on point constructors.
I don’t know whether there are reasons other than this that modules were introduced into Coq, or other purposes that other people use them for. However, over the past year I’ve discovered two other uses for them, one of which I’ll discuss in this post and another of which I’ll postpone until a later one. But first, let me tell you something about what modules are.
Coq has not just modules, but “module types”. To first approximation, it is appropriate to think of a Module Type as analogous to a Record type, and a Module having that module type (called an “implementation” of it) as analogous to an element of that record type. For instance, instead of
Record foo :=
{ bar : Type ;
baz : bar -> Type
}.
we could write
Module Type foo. Parameter bar : Type. Parameter baz : bar -> Type End foo.
and then instead of
Definition qux : foo := Build_foo Bool (fun b => if b then Unit else Empty).
we could write
Module qux <: foo.
Definition bar : Type
:= Bool.
Definition baz : bar -> Type
:= fun b => if b then Unit else Empty.
End qux.
Given these definitions, where we refer to bar qux and baz qux in the record case, in the module case we would write qux.bar and qux.baz. However, there are a few essential differences (apart from these syntactic ones).
Firstly, while elements of records are (like everything else in Coq’s type theory) strongly typed, modules are duck-typed. (Edit: Technically it may be structural typing instead; see the comments below.) In other words, qux is a module of type foo simply by virtue of containing fields named bar and baz that have the same types as those declared for the parameters of foo; the type declaration “<: foo” only serves to document and enforce this fact.
Secondly, modules do not have to be declared to have any type, or they can have more than one type. A module is free to contain as many definitions (and other things such as notations, coercions, instances, etc.) as you like, and to “implement” as many module types as you like. In particular, qux could contain additional definitions and it would still be of type foo.
Thirdly, and more importantly, modules are second-class: you cannot pass them around as arguments to functions. Nor can you construct them “on the fly”; they can only be defined at top level. (You can define them inside other modules, but not inside sections.) However, you can pass a module as an argument to another module. For instance, here is a module which takes a module of type foo as an argument.
Module htns (f : foo).
Definition qjkx : Type
:= { x : f.bar & f.baz x }.
End htns.
(Confusingly, modules that take other modules as arguments are traditionally called “functors”, but there is no requirement that they actually be functorial in the category-theorist’s sense, nor indeed do modules of a general given module-type even form a category in any nontrivial way.) Now if we have a foo, such as qux, we can pass it as an argument to htns and get a new module (again, only at top level):
Module gcrl := htns qux.
After this, we can refer to gcrl.qjkx and get { x : qux.bar & qux.baz x }. Together with the fact that modules don’t need to have a type, this sort of gives us a way to pass a module as an argument to a collection of functions; we can define a module like htns which takes a foo as an argument and in which we define many functions depending on this foo. Then whenever we want to apply these functions to a particular foo (such as qux) we do the application at top-level, as above with gcrl.
Coq does not allow modules to take elements of ordinary types as arguments. If you want to pass a nat, say, as an argument to a module, you have to first wrap the nat in another module, e.g. with
Module natM.
Parameter m : nat.
End natM.
Module timesM (mynat : natM).
Definition f : nat -> nat
:= fun n => n * mynat.m.
End timesM.
You can think of types and module-types as “parallel universes” of types; never the twain shall meet.
These limitations seem quite annoying at first. So apart from namespacing (which doesn’t generally need module types at all), why would we use modules instead of records? For modalities, the main reason is that (at least in Coq 8.5, with universe polymorphism as implemented by Mathieu Sozeau) the fields of a module are individually universe polymorphic. In other words, in order to define a module of type foo, as above, you need to give a polymorphic definition of bar and a polymorphic definition of baz, and the resulting module remembers the polymorphism of each of those fields. By contrast, a definition of an element of a record type may be itself polymorphic, but an individual instance of that definition will pertain only to a fixed collection of universes.
Note that the possibility of individually polymorphic fields practically mandates that modules must be second-class. For a polymorphic field involves an implicit quantification over all universes; hence if the record itself were a first-class object, what universe would it live in? I like to think of modules as analogous to the proper classes in NBG set theory: they can be “large” without impacting the consistency strength, because we are limited in what we can do with them. (However, this is at present only an analogy; I am not aware of any precise theoretical study of modules.)
In the case in point, if a modality were a record, then “a modality” would be a modality acting on types in only one universe. A polymorphic definition of a particular modality would result in defining related modalities on every universe, but the relation between these modalities would not be specified. In particular, if we have types X : Type@{i} and Y : Type@{j} in different universes and a map f : X -> Y, where Y is modal in Type@{j}, we could not apply the universal property to extend f to a map O X -> Y, since the universal property asserted for O@{i} X would only refer to maps with target also in Type@{i}.
This is at best annoying, and at worst unworkable. I tried for a while to make it work with various hacks, such as parametrizing a modality by two universes rather than one, but eventually I gave up. (The place where it became unworkable for me was in proving that for a left exact accessible modality, the universe of modal types is modal, which irreducibly involves applying the same modality at two different universe levels.)
Instead, we can make a modality a module. Specifically, we make Modality a module type, with each modality an instantiation of it. This means that in order to define “a modality”, you have to give a polymorphic definition of the reflector, the universal property, etc. In particular, the universal property must be polymorphic enough to allow the situation with X : Type@{i} and Y : Type@{j} considered above, and thus resolves all the problems I was having.
There are admittedly some issues involving this choice. One is the fact, mentioned above, that a module cannot be parametrized over an ordinary type. However, we do sometimes want to define a family of modalities, e.g. the n-truncation modalities for all n : trunc_index. A solution is for our basic Module Type to represent not a single modality, but an entire family of them, parametrized by some type. Thus it is actually called Modalities and contains a field Modality : Type to do the parametrization. Then we define all the n-truncation modalities at once by instantiating this module type with Modality := trunc_index. I think this can be regarded as analogous to how when doing mathematics relative to a base topos, the correct notion of “large category” is an indexed category (a.k.a. fibration), which comes with a basic notion of “I-indexed family of objects” for all I in the base topos.
Another issue is that a polymorphic field of a module must be fully polymorphic. For instance, in an instantiation of foo as above, the definition of bar must be a type that lives in every universe. In particular, therefore, one cannot define bar := Type. It would be ideal if a module type could “declare a universe parameter” that different instantiations could implement differently. This might be possible in the future, but for now I hacked around it using definitions such as Type2, which is defined by the HoTT Coq library to be a (polymorphic) universe that has at least one universe strictly below it.
A third, even more problematic, issue is that when implementing a polymorphic module type, Coq is very strict about matching up the polymorphism. Specifically, each Definition in the implementing module must have exactly the same number of universe parameters as the corresponding Parameter in the module type, and all the constraints in the former must be implied by those in the latter. This ensures that the implementation is “at least as polymorphic” as the specification, and when you think about it enough it’s hard to see how things could be much otherwise.
Normally, however, a universe-polymorphic definition in Coq ends up with many more universes than it needs, and we have little control over how many those are. Moreover, the number of universe parameters is currently rather fragile with respect to small changes. (In fact, it can sometimes happen that the interactive coqtop and the compiler coqc give the same definition a different number of universes! Although this is regarded as a bug.) Therefore, in order to have a chance of ensuring that our implementations of module types match up in polymorphism, we almost always need to add explicit universe annotations to control how many universe parameters they end up with. This is annoying and tedious, requiring much manual tracing through of proofs with copious use of Set Printing Universes and Show Universes. Moreover, sometimes a definition ends up with extra “bigger” universe parameters that can’t be eliminated, such as to serve as a “maximum” of two or more “real” universe parameters, or to serve as the target for a recursively defined type family; this sometimes forces us to hackishly introduce spurious universe parameters in our module types to match our desired instantiations.
However, universe polymorphism is a very new feature in Coq, so there’s hope that things will get better over time. It’s tempting to think the problems would be reduced with a more explicit sort of universe polymorphism such as that available in Agda (or, I believe, Lean) — but unfortunately, neither Agda nor Lean has modules that can be used in this way. Agda’s modules are more like Coq’s Sections with some additions like namespace control, simultaneous application, and binding records; in particular, there are no module types. And Lean has decided against including anything like Coq’s modules. So even though we Coq users seem to be in the minority for HoTT formalization these days, it seems I’ll be unlikely to switch my allegiance in the near future. (-:
Update: It’s been pointed out on the mailing list that while Agda’s modules can’t be used like Coq’s, Agda actually has another feature that might be usable for this purpose. Namely, in Agda there is a “” in which all the universes
live (where
is the variable that universe polymorphism quantifies over), and one can actually apply
s to types in
freely. Thus, universe-polymorphic functions, such as those that constitute a modality, can be given as arguments to a function.
It would be a little awkward because we can’t apply type constructors other than to such “large objects”, so in particular we couldn’t “package up” all the parts of a modality into a single record: any function defined for all modalities would have to take five or six arguments that make up the modality. But Agda’s modules could probably be used to reduce that annoyance somewhat.
I have not actually tried this yet, and probably won’t have time to in the near future, but if anyone else wants to I think it would be a great project.
Thanks, Mike, for the update. It sounds like the time has come to reiterate the question concerning these Coq-modules that a while back I had asked on the nForum, which was: do you have a good idea of what their categorical semantics is, hence what they mean in terms of (higher) topos theory? Is it clear, or at least plausible, that Coq code which encodes modalities in terms of Coq-modules still has the intended meaning/interpretation in terms of idempotent infinity-monads on the infinity-topos of types?
I gather from what you write here that the answer is positive and in fact quite satisfactory: Coq-modules enforce a universe polymorphism of modalities which in external higher topos language one considers anyway, and which hence has to appear in the internal formulation. Right?
Regarding your comment on Agda and Lean not supporting the kinds of modules, I have a question: when I spoke to some of the people involved in developing Lean, they told me, if I recall correctly, that part of the motivation is to redo a dependently typed programming language from scratch such as to take into account all the new insights/demands of homotopy type theory properly, cleanly and natively, thus to improve on the situation with Coq and Agda where various little hacks, fixes and deprecations are required to bring out the homotopy theory properly, due to the fact that neither of these latter two were originally designed specifically for homotopy theory.
Given that, how hard can it be for a few Lean developers to sit down and implement the module feature of just the kind required for modal homotopy type theory? Maybe if you got in touch with them about this, they could easily provide a custom-made feature that would actually improve on the modulefeature as offered by Coq?
Just a thought. Of course I may be way off here, not really knowing all the nitty-gritty details involved. I just thought that particular idea of the Lean project sounded like a really good one.
I would say that I have a reasonable idea, but hardly anyone seems to have studied this question precisely. One possibility would be to suppose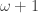 universes and let the universe-polymorphic objects belong to the
universes and let the universe-polymorphic objects belong to the 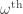 . That wouldn’t handle the other use of modules (for comodalities) that I hope to blog about sometime later, though.
. That wouldn’t handle the other use of modules (for comodalities) that I hope to blog about sometime later, though.
When I asked Bob Harper about the semantics of modules, he pointed me to this paper by Moggi and this followup with Harper and Mitchell. They are mainly focused on modules in ML and aspects such as maintaining the compile-time / run-time phase distinction, which is less relevant for MLTT, but they should be a good starting point for someone to give a category-theoretic semantics of Coq modules.
I certainly find it very plausible. And in the case of any particular modality that one can construct internally, like the n-truncation or the localization at some type family, I think it is more or less clear that we get what we expect, since the module application can be beta-reduced away. But answering this for the case of a generic module would require a general categorical semantics of modules.
My impression is that it might be quite hard, at least if they were trying to mimic the behavior of Coq’s modules. I’m told that the implementation of Coq’s modules is actually quite complicated, infects the entire kernel (making it more difficult to alter other aspects thereof), and is only fully understood by a handful of people (if that). When this question was raised on the lean github project, Maxime Denes (one of the Coq developers) had this to say:
This led to the decision not to implement such modules in Lean. It’s possible that there would be some less-invasive way for Lean to allow universe-polymorphic hypotheses, but if so I don’t know what it is.
Thanks. Interesting to see that exchange, or rather the lack thereof, about the implementation of modules in Lean. So the suggestion there that “an elaboration to dependent records would have been enough” you’d not subscribe to?
He said it would have been enough “for most usages”, which I can readily believe. But it wouldn’t be enough for this usage, unless it were a much more elaborate elaboration than I expect he intended.
I expect that probably part of the problem with Coq modules is that they’re trying to be too many things at once. For modalities, and more general universe-polymorphic hypotheses, I feel like what we need is a sort of “reified metatheory” (akin, again, to NBG), and there’s no a priori reason that that needs to have anything to do with the sort of namespacing uses that modules are usually put to.
Great, so maybe _that_ statement needs to be passed to the HoTT-aware Lean developers.
Maybe. I haven’t done so myself, because I think it wouldn’t be very likely to succeed without a more concrete suggestion to back it up. “We need some way to reify the metatheory” sounds more like a proposal for a research project than a request for a software feature.
The statement I meant was: admit “universe-polymorphic hypothesis”. That sounds quite like a sensible feature request.
By the way, a while back here
https://groups.google.com/forum/#!searchin/hott-cafe/Stokes/hott-cafe/3hC942yNcU4/aAAQlITUtcoJ
you had asked people to wait for you to complete some rewriting of the modalities libraray before embarking on doing anything with them (hm, did my original message, the one that the above link is the reply to, disappear from the list?). I suppose that time has come now?
It may sound like a sensible feature request, but I don’t think it is one, because it would require a substantial amount of new theory to be developed first. In other words, it’s a feature request to ask of a type theory, not of an implementation of a type theory, and the Lean folks are writing a new implementation rather than a new type theory.
Yes, have at your modalities now. The comodalities for cohesion aren’t quite in the library yet, though; I’ll be submiting them soon (I hope — it’s depressing to be reminded that back in October I was hoping to be done in a few weeks) and making another blog post.
However, you’ve motivated me to start a discussion about whether there may be other ways to get such a feature, so thanks! I’ll move it to the mailing list.
It turns out that Agda has a different feature that might be usable to implement universe-polymorphic modalities. I updated the post with a few paragraphs at the end. Do we have anyone here qualified to comment on whether Lean might support a similar feature?
Hi.
From my reading of the duck typing article, it sounds like a form of dynamic typing. This doesn’t seem to be what’s going on with Coq modules, since module parameters still have module types.
Instead, Coq modules seem to be using some kind of record subtyping, so modules can be upcast to the type they’re used at. When providing a module as an argument, that type is the parameter module type.
My point about duck typing is that you don’t have to declare a module as having any module type at all; it automatically has any module type that it satisfies the signature of. That is, if you have a module type duck with one parameter quack, then any module defining a field quack with the same type automatically has the module type duck, and can be passed to any module function that expects a duck. Possibly I should be talking about “structural typing” instead? From a quick perusal of wikipedia (not always the most reliable source), it seems that perhaps the only difference between the two is compile-time versus run-time, which gets blurry in a dependently-typed language anyway.
Right. That’s what record subtyping gets you. It infers a minimal type based on the module definition, and the module automatically also has any type that’s a supertype.
Maybe. Depends on which Coq command you believe regarding which modules have which fields. Consider this example:
Printseems to thinkQuackerhas aquackfield. But the type checker doesn’t. Alternatively, I’d explain the problem as USELESS is not a subtype of DUCK.This module typing is structural, but I think the subtyping is what’s causing the behavior you’re talking about. And structural typing need not involve subtyping.
Because module parameters have types, it seems clear that this is not dynamic typing. With dynamic typing, a module function would not be “type checked” until it’s applied, so it would not need a module type annotation for its parameter. It would simply use the type of whatever module it’s given.
Oh, right. Because I never use it (and I can’t really imagine why anyone would), I tend to forget that Coq also lets you declare a module and make its insides completely invisible except for the fact that they instantiate a particular module type. That’s what Quacker : USELESS does. If you change your definition to Quacker <: USELESS, which is the syntax I always use (except when I forget to, and get confusing error messages until I remember), then I think it will compile just fine.
It’s a way to isolate the rest of the program from the implementation details of a module without having to wrap the rest of the program in module functions. But maybe that isn’t a good idea, since it still wouldn’t let you instantiate the rest of the program with multiple modules.
Right. The point is that while you don’t have to declare a module’s type, you can, which I thought would demonstrate that it isn’t duck typing. And for a module parameter, it seems you have to.
Maybe this demonstrates it better:
My understanding is that if module typing were duck typing, this would’ve worked, because we do pass
DuckUsersomething that quacks like a duck. Of course the checker never gets that far, because it’s doing static checking.(Really I never understood how the duck analogy is supposed to explain anything. I’m going on the impression that duck typing is dynamic typing.)
Maybe we should stop arguing about something that neither of us fully understands, then. (-: Are there any experts around who can straighten us out?
I would have said that the declaration : USELESS means that Quacker doesn’t actually quack like a duck. It may “internally” know how to quack but that’s an implementation detail; as an object visible to the outside, it doesn’t quack, so we shouldn’t expect to be able to pass it to something that needs a duck.
And I would have said that the module-type of a module parameter is just checked documentation for the fields that have to exist in that parameter. The error in your second example is not that you didn’t pass DuckUser something that can quack — you did — but rather that when you defined DuckUser you claimed that its argument wouldn’t need to be able to do anything, but then violated that contract by asking its argument to quack.
What I’m not sure about is what counts as duck typing. But I’m sure Coq’s module typing isn’t dynamic typing.
Since the Wikipedia article you linked presents duck typing as a sort of dynamic typing, I concluded that it’s probably not what you meant. So personally, I’d refer to it as something else, or find a better reference for the kind of duck typing you mean. I still think it’s best explained by record subtyping though.
But yeah, we’re arguing over a small detail. What’s important is that you figured out how to use modules for what you need, which is good.
Well, I’m not sure how to decide whether anything in Coq is “dynamic” or not, since there isn’t really a compile/run time phase distinction at all. And stackoverflow doesn’t seem to have a consensus on whether duck typing is dynamic or not (one, two). But perhaps it would have been more correct to say “structurally typed“, although wikipedia doesn’t even agree with itself about whether that is different; the page on subtyping refers to structural subtyping as “This so-called duck typing”. I do think that the behavior in question falls under the informal description of duck typing (“if it quacks like a duck, I can use it like a duck”), whether or not it’s included by the “official” definition of duck typing (insofar as there might be one).
Well runtime type checking doesn’t mean exactly the same thing as dynamic typing to me. If you have runtime compilation and loading, you might type check the code when you compile it, at runtime. So that’s runtime type checking, but it’s not dynamic typing, because the code being checked is not running yet.
In other words, with dynamic typing, a having a type error is a property of an execution of a program, not of the program itself. The fact that Coq rejected the definition of DuckUser, so that I don’t even get to “execute” it on Duck, shows that this is not dynamic typing, whether or not you consider it to be happening at runtime.
Thank you for finding these. They echo my own uncertainty about what “duck typing” is supposed to mean. Maybe it’d be best to classify Coq’s module typing as structural subtyping, rather than either duck typing or record subtyping. (It’s still essentially record subtyping, but since your post is contrasting modules and records, it’d be confusing to call it that. Of course Gallina records don’t have record subtyping, but still…)
I don’t know of any “official” definition of duck typing. It seems to me more like a marketing term to appeal to people fed up with Java than a well-defined class of type system phenomena. Another reason to use a different term.