A few days ago Martin Escardo asked me “Do idempotents split in HoTT”? This post is an answer to that question.
Coherent idempotents
To start with, what is an idempotent? The standard meaning of idempotent is a map such that
, which in HoTT would mean a homotopy
. A splitting of an idempotent is a pair of maps
and
such that
and
. (Note that the existence of such
actually implies
is idempotent, since then
.)
Given an idempotent in HoTT, the obvious way to try to split it would be to take , with
and
. However, with this definition we cannot in general prove
. Indeed, as Martin pointed out, when
with the obvious proof of idempotency, for this definition to satisfy
is the same as to say that
is a set.
This suggests that if is not a set, then we might need some sort of coherence for the witness
of idempotency. For instance, we might ask whether
. And if we had a witness of that, then we could ask for that witness to satisfy some further condition, and so on off to infinity.
To see that such extra conditions are necessary, we can observe that they hold for any split idempotent. That is, suppose we have and
and a homotopy
, yielding as above a witness that
is idempotent. Then the naturality of H implies that the coherence condition
also holds, and we can continue on as far as we like.
It’s important not to read more into this observation than it says. What it says is that if a function f can be written as for functions s and r such that
, then f admits a “coherent system of idempotence data”. It doesn’t say that if f is idempotent with a specified homotopy
and f splits, then I must itself be coherent. Therefore:
- Even though a split idempotent automatically gives rise to an infinite system of coherence data, it doesn’t follow that in order to construct a splitting we would necessarily need to give an infinite system of coherence.
- It’s not too hard to give examples of homotopies
that are not coherent, but it’s rather less obvious how to give an example of an incoherent idempotent for which there doesn’t exist some other homotopy that is coherent.
Fortunately, Jacob Lurie has already studied the analogous questions in -category theory. In Higher Algebra he showed that if a witness to idempotence satisfies the one additional coherence condition
, then the idempotent f can be split, and hence admits some coherent system of idempotence data (which, apparently, may not be the same as the original one). He also gave an example of an incoherent idempotent that does not split, and hence does not admit any coherent system of idempotence data.
In the rest of this post I will describe proofs of the analogous facts in HoTT, inspired by Lurie’s categorical ones (but not quite identical to them, even under the categorical semantics of HoTT). I have verified it all in using the HoTT/Coq library; pull request is here.
Splitting coherent idempotents
Firstly, suppose we have an idempotent , with witness
and single coherence
. Lurie constructs a splitting as the colimit of the sequence
We could probably do the same in HoTT, using a HIT for the colimit. However, idempotents are self-dual, so we could just as well consider the limit of the sequence
and this is rather easier to work with in HoTT; it’s just
If we call this type , then we have an obvious
defined by
, and a slightly less obvious
defined by
, such that
. The tricky part is proving
. (Of course we need function extensionality at this point.) By definition,
, so we need to show first of all that
for all
. We induct on
. The base case is
where the middle equality is and the other two are the specified equality
(part of the second component of
). The induction step is similarly
using the induction hypothesis at the end. It remains to check a naturality condition, than the composite is equal to the composite
, and we can similarly do this by induction. The details are left to the reader (or you can find them in the formalization). Of course, we have to use the coherence
in there somewhere. One might say that we only need one level of coherence “because” of the induction: we can apply
once at each induction step and build up more and more coherence as
increases.
I have not fully digested the rest of Lurie’s proof; once I got the idea of the sequential limit, I put down his book and constructed the rest of the above proof myself in “HoTT-style”. It could be that when compiled out categorically, it will yield the dual of Lurie’s proof; or it could be that they are honestly different.
An incoherent idempotent that does not split
Lurie’s example of an “irreedeemably incoherent idempotent” lives on , where
is the topological unit interval (not to be confused with the HIT interval) and “Aut” denotes its group of self-homemorphisms. However, after digesting the example, I think it’s even more natural to replace the unit interval with Cantor space
. In particular, the topology plays no role in the counterexample (although in constructive models
does of course behave “topologically”).
By definition, in HoTT by we mean
. Topologically, this is the “classifying space for fibrations with fiber
“. It is connected and pointed (with basepoint
), and its loop space is the type
of self-equivalences of
. Thus, if
is a set (such as Cantor space
), then
is a
, where
is the (set-)group
.
In particular, a map is determined essentially by a group homomorphism
. This is how Lurie talks about it: in the case
he defines the action of
on an automorphism
by
if
and
otherwise. For
, we could define an analogous
by
if
and
if
. In other words, we use the fact that our space decomposes into two copies of itself, and we have our automorphism
act on the first copy only.
Now, actually defining like this in HoTT would require knowing that endomaps of
correspond to group endomorphisms of
. The only way I can think of to do this is to construct
as a HIT, show that it’s equivalent to
, and then use the recursion principle of that HIT. (Is there’s another way?)
However, our definition of suggests an alternative approach. An element of
is a type
that is merely isomorphic to
; let’s just define
(where from now on
will be the Cantor space). Note that the action of this
on automorphisms is, roughly, what we described explicitly above: it takes an automorphism and restricts it to act on the “first copy”. The fact that
decomposes as two copies of itself,
, implies that
is in fact an endomorphism of
, since we have (merely)
. And the same fact implies that
is idempotent, since
. I think this is a nice example of the benefits of the univalent approach to classifying spaces!
It remains to show that is not coherently idempotent. Lurie says that if it were, then the colimit
would be its splitting, and hence the map from
to that colimit would be surjective on
, whereas
itself is certainly not surjective on
and so this is impossible. In HoTT, this would requite a HIT colimit, and probably an encode-decode argument to characterize the
of the colimit.
However, here again we can give a more direct argument. Suppose were coherently idempotent, so that we have
and
. The coherence
is an equality in the type
, thus it is equivalently a homotopy between two equivalences
. Essentially by definition, the first equivalence (corresponding to
) decomposes the domain and codomain as
and
, mapping the first summand
to
by
and the second summand
to
by the identity.
As for the other, if were the idempotency proof
that we gave above, then the equivalence
corresponding to
would bracket the domain instead as
and map it to
by the identity on
and the “fold” equivalence
. Thus, the two could not possibly be homotopic, since they would send the third summand of
to different summands of the codomain.
This argument doesn’t quite work as stated since might not be the same proof of idempotency that we gave above. However, whatever
is, it’s defined “for all
“, which by the HoTT meaning of “for all” implies that the induced equivalences
must be natural with respect to automorphisms of
. In particular, the equivalence
induced by
must be natural with respect to the “flip” automorphism
. By looking at which summands are fixed by the automorphisms induced by this flip, we can conclude that
must map the last two summands in the domain to the last one summand in the codomain, just as our original proof of idempotency did. Thus, our previous argument to a contradiction kicks in. Again, the details can be found in the formalization.
Open questions
There are a number of further questions to ask. For instance, if we have and we use them to split
, do the new witnesses
induced from the splitting agree with the given ones? How many different ways can a given map
“be idempotent” — can you give an example of a map that is idempotent in two genuinely different ways, perhaps with non-equivalent splittings?
Here’s one I’d especially like to know the answer to. There is an arguably more obvious way to try to split a coherent idempotent: instead of the naive definition , we can try to add an extra level of coherence corresponding to
and ask for
. I tried this first, but the path algebra involved in showing
was just too much for me. I was able to show that it works when
is the identity function, though, which is promising. Can anyone either show that it works for general
, or exhibit an
for which it doesn’t work?
Very nice! Thanks for such a complete answer.
I would like to record a special case of interest that has a more direct proof. Suppose you instead ask
Which functions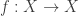 split with a section-retraction pair
split with a section-retraction pair  and
and 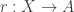 such that
such that  is an embedding in the sense of the HoTT book?
is an embedding in the sense of the HoTT book?
This means that the application map is an equivalence, or, equivalently, which is what I am going to use, the fibers of
is an equivalence, or, equivalently, which is what I am going to use, the fibers of  are propositions. Then the answer to the above question is
are propositions. Then the answer to the above question is
Precisely those idempotents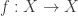 such that the type
such that the type  has split support for every
has split support for every  .
.
The proof is easy. In one direction, consider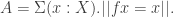 Then the obvious section and retraction work. For the other direction, we have to show that if
Then the obvious section and retraction work. For the other direction, we have to show that if  does split in the above manner, then the type
does split in the above manner, then the type  has split support. Because
has split support. Because 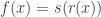 , it is enough to show that the type
, it is enough to show that the type  is logically equivalent to a proposition. But it is easy to see that it is logically equivalent to the fiber
is logically equivalent to a proposition. But it is easy to see that it is logically equivalent to the fiber 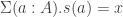 , which is a proposition, by assumption.
, which is a proposition, by assumption.
Thanks for adding this! It emphasizes in another way the different behavior of idempotents in homotopy theory, since in set theory, the splitting of an idempotent is always a subset of the original carrier.
Are there any non-sets that have the property “ has split support for every x” in an interesting way? As an example of a boring way this could happen for a non-set, we could consider
has split support for every x” in an interesting way? As an example of a boring way this could happen for a non-set, we could consider 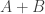 , where B is a set and f maps A into B.
, where B is a set and f maps A into B.
If f is the identity, then this property just says that we have . Of course that’s true trivially for all X (as it must be, since the identity splits by a pair of identity maps), and can also be true non-trivially, such as when
. Of course that’s true trivially for all X (as it must be, since the identity splits by a pair of identity maps), and can also be true non-trivially, such as when  or
or 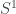 .
.
Another remark: Notice that the type constructed in my proof is (equivalent to) the image of the idempotent
constructed in my proof is (equivalent to) the image of the idempotent  , and that the section-retraction pair is simply the canonical factorization of
, and that the section-retraction pair is simply the canonical factorization of  through its image. Conversely, if the canonical factorization of a function
through its image. Conversely, if the canonical factorization of a function  through its image is a section-retraction pair, then the type
through its image is a section-retraction pair, then the type  has split support for every
has split support for every  (either by direct calculation, or using the fact that the image is always embedded). For a constant map, to use Nicolai’s example below, the image is not in general contractible, but the splitting is through a contractible type.
(either by direct calculation, or using the fact that the image is always embedded). For a constant map, to use Nicolai’s example below, the image is not in general contractible, but the splitting is through a contractible type.
Nice, I have enjoyed this! I have not fully digested some parts of your post, but I think I can answer your last question:
First, I have a simple positive statement: has the property that the map
has the property that the map 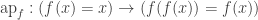 is an equivalence for all
is an equivalence for all  (and
(and  also comes with
also comes with  and
and  , of course!), then what you said works.
, of course!), then what you said works. , the type
, the type  will be contractible (it is essentially a coconut – it would be a “pure” coconut if the
will be contractible (it is essentially a coconut – it would be a “pure” coconut if the  was removed and the
was removed and the  replaced by some other fixed term to make it type check; but because of our assumption,
replaced by some other fixed term to make it type check; but because of our assumption,  does not make a difference). So,
does not make a difference). So,  and
and  are equivalent and the equivalence is the first projection. Thus, to convince ourselves of
are equivalent and the equivalence is the first projection. Thus, to convince ourselves of  , we only need to check that the first component of
, we only need to check that the first component of 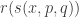 equals
equals  , but this component will be
, but this component will be 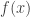 , and the required witness is
, and the required witness is  .
. , and in particular for the identity.
, and in particular for the identity.
If
We can see this as follows: for any given
Of course, this means that what you suggested works for all embeddings
Now one should probably wonder whether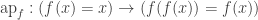 might be always an equivalence. After all, if we have some
might be always an equivalence. After all, if we have some  , then the types
, then the types 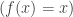 and
and  are equivalent. Unfortunately,
are equivalent. Unfortunately,  is not necessarily an equivalence anyway.
is not necessarily an equivalence anyway.
If I have not made a mistake, I can give an example in which the suggested does not work. Suppose
does not work. Suppose  is some type with a point
is some type with a point 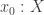 . Define
. Define 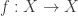 to be constantly
to be constantly 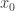 . Then,
. Then,  is idempotent with the witness
is idempotent with the witness  being constantly
being constantly  , and the coherence proof
, and the coherence proof  can be taken to be constantly
can be taken to be constantly  as well. Now the type
as well. Now the type  simplifies to the coconut
simplifies to the coconut 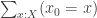 . Set
. Set  as in your question. We know that
as in your question. We know that 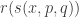 will be
will be 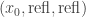 . We further know now that the two pairs
. We further know now that the two pairs 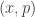 and
and  live in a contractible type. The equality
live in a contractible type. The equality  can therefore be simplified: we can assume that
can therefore be simplified: we can assume that 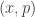 is actually judgmentally
is actually judgmentally  , and then the equality of the triples is equivalent to the equality
, and then the equality of the triples is equivalent to the equality  . This is the case if
. This is the case if  is a 1-type, but of course not in general.
is a 1-type, but of course not in general.
Nice; thanks! I should have thought to look at constant maps (being the “polar opposite” of the identity map). So I guess the sequential limit construction is it. On one hand, this makes sense to me, because just as a “coherent idempotent” ought to involve infinitely many data, I feel that an element of its splitting ought also to involve not just a path but infinitely many coherence data on it. And an element of the sequential limit does involve infinitely many data. But on the other hand, it doesn’t make sense, because the data in a point of the sequential limit are all points and 1-paths; there are no higher coherence paths visible. Are they hidden somewhere?
but infinitely many coherence data on it. And an element of the sequential limit does involve infinitely many data. But on the other hand, it doesn’t make sense, because the data in a point of the sequential limit are all points and 1-paths; there are no higher coherence paths visible. Are they hidden somewhere?
I’m making a bit of progress on the other questions I asked. In particular, I can now prove that the idempotence datum is recoverable from the splitting, and I have a guess for a counterexample to show that
is recoverable from the splitting, and I have a guess for a counterexample to show that  is not generally recoverable. Once I’ve sorted it all out, I may make another post.
is not generally recoverable. Once I’ve sorted it all out, I may make another post.
It is probably somewhat obvious, but I cannot see what the canonical next coherence condition (after ) is, or how
) is, or how  should be extended. Can you give me a hint?
should be extended. Can you give me a hint?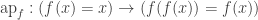 is an equivalence”, but together with “
is an equivalence”, but together with “ is idempotent”, this already implies that
is idempotent”, this already implies that  is the identity. Martin and I noticed this.)
is the identity. Martin and I noticed this.)
(Side note: In my first comment I said that the splitting works under the condition “
It’s actually a bit of an accident that can be given such a short type. Really,
can be given such a short type. Really,  should be a homotopy between the two induced homotopies
should be a homotopy between the two induced homotopies  , one of which is
, one of which is  and the other of which is
and the other of which is  . But since whiskering with
. But since whiskering with  is an equivalence, it’s equivalent for
is an equivalence, it’s equivalent for  to relate
to relate 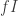 and
and  .
.
As we go up in dimensions we can formulate the conditions as cubes or as simplices. With cubes, we would regard in the form
in the form 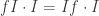 as a square, draw a cube whose faces are all instances of this
as a square, draw a cube whose faces are all instances of this  (except that one of them is a naturality square), and ask for the next coherence datum that fills in this cube.
(except that one of them is a naturality square), and ask for the next coherence datum that fills in this cube.
With simplices, the dimensions are shifted by one: we regard as a 2-simplex with boundary 1-simplices
as a 2-simplex with boundary 1-simplices  , then
, then  is a 3-simplex whose boundary 2-simplices are
is a 3-simplex whose boundary 2-simplices are  , and then the next datum is a 4-simplex whose five boundary 3-simplices are instances of
, and then the next datum is a 4-simplex whose five boundary 3-simplices are instances of  (in this case the naturality is invisible).
(in this case the naturality is invisible).
Thanks! I managed to draw these (up to the three dimensional case). But why did you say that there are no visible higher coherence paths? gives paths,
gives paths,  gives paths between paths, and so on. Which sort of paths would you have expected?
gives paths between paths, and so on. Which sort of paths would you have expected?
I mean that in the construction of a splitting of an idempotent as a sequential limit, which I described in the post, there are no visible higher coherence paths. I would naively have expected an element of the splitting to consist of a point and a path
and a path 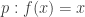 and a homotopy
and a homotopy  , a higher homotopy involving
, a higher homotopy involving  , and so on, including paths of all dimensions. Instead, an element of the splitting consists of a function
, and so on, including paths of all dimensions. Instead, an element of the splitting consists of a function  and a family of paths
and a family of paths 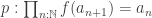 , all of which are just 1-dimensional paths.
, all of which are just 1-dimensional paths.
Oh, I see. Thanks.
I’ve now posted a preprint based on the results of this blog post and its sequel; it’s available at arXiv:1507.03634. In addition to the contents of the blog posts, the paper contains