Lenses are a very powerful and practically useful functional construct. They represent “first class” fields for a data structure.
Lenses arose in work on bidirectional programming (for example, in Boomerang), and in Haskell, people have given many different definitions of lenses, but the simplest and easiest to replicate in type theory is probably the one based on getters and setters.
Given types and
, a lens from
to
is given by the following data:
- a function
, the “getter”;
- a function
, the “setter”;
subject to the following laws:
says that we get what we put in,
says that updating with the current value doesn’t do anything,
says that if we update twice, only the last update counts.
This definition makes sense for general types and
, and it’s straightforward to define composition for those lenses. However, as soon as we try to show – say – that composition is associative, we stumble upon “coherence” issues.
The problem with this definition becomes apparent if, following Russell O’Connor, we think of the pair as a coalgebra of the costate
-comonad
defined by:
The laws that we specified are only enough to show that is a
-coalgebra, which is not a well-behaved notion, unless we restrict our attention to sets (i.e. 0-truncated types).
Unfortunately, it is not yet clear how to define -categorical concepts internally in HoTT, but we can try to restructure the definition to work around the need to deal with higher coherences.
One possible idea is the following: a function is the getter of a lens if we can “coherently move” between any two fibres of
. This can be made precise by asking that
is the pullback of some map
along the projection
.
So we arrive at the following definition: a higher lens is a function such that the family of fibres of
:
factors through .
At this point, we need to show that for any two sets and
, a higher lens from
to
is the same as a lens.
Suppose is a higher lens, and let
be a morphism that factors
. Given
, we have that
By applying we get an equivalence
between
and
.
Therefore, for any and
, we get:
We can now define:
and obtain the setter and the first law at the same time.
To get the other laws, we observe that the are coherent, i.e. given
,
from which the third law follows easily. For the second law, it is enough to observe that coherence implies that is the identity.
So, any higher lens is also a lens, regardless of truncation levels.
Now, let and
be sets, and
a lens from
to
. The family of fibres of
can be thought of as having values in the universe
of sets, which is a 1-type. We are now left with the problem of factoring the map
from
to a 1-type through
.
Nicolai Kraus and I are currently working on a paper on precisely the topic of factoring maps through truncations, where we give, for any and
, a necessary and sufficient condition for a map from some type
to an
-type to factor through
.
In our case, we have and
, and in this particular example, the condition is as follows: we first need a “0-constancy” proof for
:
and then a “coherence” property for :
Together, and
form what we call a “1-constancy” proof for
.
To show that is 1-constant, we begin by defining a map between any two fibres of
:
and showing that it is functorial, in the sense that we have functions:
These can be obtained simply by reversing the above derivation of a lens from a higher lens and using the fact that both and
are sets. Now,
is easily seen to be an equivalence (its inverse being
), giving
, and then
follows directly from
.
We haven’t shown that these two mappings are inverses of each other. I haven’t checked this in detail, but I think it’s true. To prove it, one would need to rearrange the above proof into a chain of simple equivalences, which would directly show that the two notions are equivalent.
A lens from A to B can also be represented by the type
Lens A B = exists C. Iso A (B × C)
Where Iso represents isomorphisms. The lens laws are equivalent to the laws of isomorphisms.
In HoTT the Iso could be replaced with equivalence or even equality (by univalence). I haven’t given it much thought, and I don’t understand much of the category theoretic language used in this post, so I don’t know what happens to higher paths. Also one problem of this definition is that it is large.
Yes, this is the intuition behind my definition: I’m trying to capture the idea that is a “trivial” fibration (in the sense that it’s a product, not that it’s acyclic).
is a “trivial” fibration (in the sense that it’s a product, not that it’s acyclic).
However, I don’t think you can really take that as the definition, since it doesn’t work when A and B are empty (you get the whole universe instead of the unit type).
How does this connect to dependent lenses ?
I didn’t know about that development. Interesting.
In any case, the lenses I defined in this post are non-dependent. I’m actually not sure what dependent lenses should actually be, since any function could be considered as the getter of one (you can always express
could be considered as the getter of one (you can always express  as a sigma type of the fibres of
as a sigma type of the fibres of  ).
).
As an example, what would g’ : A’ -> || B || be if we take g to be g : X x Y -> X; g = fst ?
Also, is this way of getting around the need for coherence laws an instance of a more general technique?
My reply is below.
For , the fibres are all equivalent to
, the fibres are all equivalent to  , so
, so  is just
is just  , corresponding to the map
, corresponding to the map 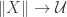 constant at
constant at  .
.
I don’t think this is an instance of a general technique. Sometimes, there really is no way of avoiding coherences, which usually means that you cannot work internally anymore, at least not until we figure out a way to internalise semi-simplicial sets or similar constructions.
In this case, we are lucky, since we can reduce the particular tower of “coherence properties” we want to asking that a certain map be “constant” in a strong sense (i.e. factor through the -1-truncation of its domain). In practice, however, expressing such a constancy property explicitly would require you to go back to the infinite tower of coherences (at least in the case where you make no assumptions on the truncation levels of the types involved).
I don’t suppose your necessary and sufficient conditions for factoring through truncations will apply to the case ?
?
They do, with some caveats.
The idea (for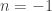 ) is as follows: given a type
) is as follows: given a type  , we can construct a corresponding semi-simplicial type in two ways. One is to make it into a 0-coskeletal semi-simplicial type
, we can construct a corresponding semi-simplicial type in two ways. One is to make it into a 0-coskeletal semi-simplicial type  (whose component at level
(whose component at level  is simply
is simply 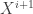 ). The other is to take the constant presheaf at
). The other is to take the constant presheaf at  and then take a Reedy fibrant replacement (for which we use an explicit construction). Let’s denote this by
and then take a Reedy fibrant replacement (for which we use an explicit construction). Let’s denote this by 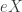 .
.
Then, a function factors through
factors through 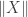 if and only if it can be extended to a presheaf morphism
if and only if it can be extended to a presheaf morphism  . This turns into a tower of coherence conditions for
. This turns into a tower of coherence conditions for  , which can be simplified to a finite one when
, which can be simplified to a finite one when  is
is  -truncated.
-truncated.
We still have to work out some of the details of the proof, so I’m currently not particularly confident about the exact requirements. We definitely need Reedy limits of towers, and the general case uses certain HITs. We also use strict functoriality of path objects quite liberally, but that could possibly be avoided.
uses certain HITs. We also use strict functoriality of path objects quite liberally, but that could possibly be avoided.
Right, that’s what I would expect. That construction for n=-1,0 and m=0,1 can essentially be found in the book (m=0 via exactness of the category of sets, so that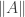 can be constructed as the set-coequalizer of
can be constructed as the set-coequalizer of 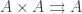 , and m=1 via the Rezk completion, with 1-types viewed as groupoids). Mainly I was wondering whether you’d found a way to express the infinitely many coherence conditions for
, and m=1 via the Rezk completion, with 1-types viewed as groupoids). Mainly I was wondering whether you’d found a way to express the infinitely many coherence conditions for  internally; but if you can express the case of finite m as an internal function of m, that’s pretty impressive too!
internally; but if you can express the case of finite m as an internal function of m, that’s pretty impressive too!
How do you use the Rezk completion to prove the factorization property for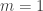 ? I’m afraid don’t see it. I’m also not sure about the argument for
? I’m afraid don’t see it. I’m also not sure about the argument for 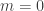 , because
, because  doesn’t need to be a set for
doesn’t need to be a set for 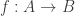 to factor through
to factor through  , but maybe I just misunderstood what you meant.
, but maybe I just misunderstood what you meant.
Unfortunately, we cannot express the case of finite as an internal function of
as an internal function of  . Actually, I think that if we had that, we could easily express the
. Actually, I think that if we had that, we could easily express the  case as well, since Reedy limits of “internal” towers do always exist.
case as well, since Reedy limits of “internal” towers do always exist.
We have been toying with the idea of writing some code generator that would give us the statement (and proof!) for any fixed and
and  , so that you could plug it into a proof assistant and use it in practice, assuming the truncations levels are known statically. I don’t know how useful/interesting that would be.
, so that you could plug it into a proof assistant and use it in practice, assuming the truncations levels are known statically. I don’t know how useful/interesting that would be.
To have a proper internal formulation of this result, I think we really need something like the universe of semi-simplicial types. I have been experimenting with adding ad-hoc rules into the syntax that would allow us to take Reedy limits over arbitrary (countable) inverse categories (as I briefly mentioned in a comment to your own post), but I’m still not sure if and how that would work.
Just 0-truncate it first: since B is a set, f automatically factors through .
.
For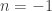 and
and 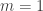 , let A be the codiscrete precategory with A as its type of objects, i.e.
, let A be the codiscrete precategory with A as its type of objects, i.e.  for all x,y. Then the Rezk completion of A is the (-1)-truncation of A. Let B be the “discrete” category with B as its type of objects, i.e.
for all x,y. Then the Rezk completion of A is the (-1)-truncation of A. Let B be the “discrete” category with B as its type of objects, i.e.  for all x,y. Since B is a category, a functor
for all x,y. Since B is a category, a functor 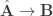 can be induced by a functor
can be induced by a functor 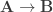 , which is basically what you called a “1-constancy proof”.
, which is basically what you called a “1-constancy proof”.
For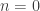 and
and 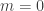 , let A be instead the “discrete” precategory on A, with
, let A be instead the “discrete” precategory on A, with 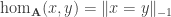 . Now the Rezk completion of A is the 0-truncation of A.
. Now the Rezk completion of A is the 0-truncation of A.
I don’t see that; can you elaborate?
Oh, of course! Thanks. That’s exactly the specialization of our proof, by the way. I didn’t recognize the Rezk completion in there.
Well, I meant that one can use coinduction to take the limit of such a tower of coherences. I’m not sure what is known about the existence of coinductive types in models of HoTT, so this might not be a big improvement, but at least we have some syntax to talk about such things.
In fact, suppose the property is expressed by a term
P : (n : Nat) -> E n -> Type
where E satisfies:
E 0 = 1
E (suc n) = Sigma (x : E n) . P n x
definitionally.
Then you could give a definition like:
codata S (n : Nat)(x : E n) : Type where
cons : (y : P n x) -> S (suc n) (x, y) -> S n x
and S 0 * would give you the limit of the tower.
I mean, how do you know that the limit of that tower would give you the condition that works for ?
?
Oh, that’s what we prove (assuming all the details work out… as I said, it’s work in progress): the type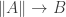 is equivalent (over
is equivalent (over  ) to the Reedy limit of a certain tower, provided such limit exists.
) to the Reedy limit of a certain tower, provided such limit exists.
The way I phrased it was indeed weaker, but this is the formulation we are aiming for.
Okay; I look forward to seeing the proof! I can’t think of a way to prove that without having a “geometric realization” for untruncated simplicial objects, which at least naively would be a HIT with infinitely many constructors.
There is a new paper on lenses at TYPES.