In the last year, I have written my master thesis on homotopy type theory under supervision of Andrej Bauer in Ljubljana, to whom I went on an exchange, and Jaap van Oosten and Benno van den Berg in Utrecht. Their reactions, and Steve’s, have encouraged me to share it here on the HoTT blog. So here it is:
hott.pdf (revised version)
In this blog post I give a brief outline of the things I included in my thesis:
- Since I had no knowledge of type theory before I started on this project, and none of my fellow students have it neither, I have written my thesis as an introduction and a short chapter on pre-homotopy type theory is also included.
- In chapter 2 the theory of identity types is presented, with most of the material of the Coq repositories included. Some noteworthy things from this chapter are: theorems which state the equivalence of the spaces of “data needed to construct a section of P” and of sections of P for each dependent type over an inductively defined type (the uniqueness up to equivalence of an inductively defined space is derived from such theorems), two applications of the Univalence axiom and the type theoretical Yoneda Lemma, about which I have posted before. Another thing is that I have tried to write fluently about homotopy type theory.
- In chapter 3 higher inductive types are introduced. After the definition of a hit, there is again a theorem which states the equivalence of the spaces “data needed to construct a section of P” and of sections of P, so these carry over to the higher inductive types. Once there is a general way of saying what the higher inductive types are, it should be possible to deduce such a theorem in more generality. In this chapter there are also the proofs that the fundamental groupoid of the circle is the integers (see Shulman’s post) and that the omega-sphere is contractible (Brunerie).
This is excellent! I think this may potentially be a big help to newcomers trying to understand HoTT. I also like your theory of adjunctions; it’s nice that you can get so much without needing a “coherently homotopical” notion of adjunction.
I’ve only just skimmed it, but here are a few minor comments:
I don’t think you ever stated explicitly that function-types associate to the right, and that that’s how we deal with multi-argument functions. A reader not familiar with that idea may be a bit confused.
The first sentence of chapter 2 doesn’t sound quite right to me; I think “intensional type theory” refers to a particular mode of behavior of identity types (and perhaps other things as well), not to the mere existence of identity types.
There are a lot of references showing as ??, as if you need to run LaTeX again. This makes, e.g., the proof of 2.3.17 quite difficult to follow! (-:
There are a bunch of typos; the most confusing one I saw is in the sentence prior to 2.7.10, where one of the words “dependent” should probably be “non-dependent”. A similar one is in the second paragraph of chapter 3, where probably “we do have” should be “we do not have”.
The symbol usually used for adjunctions is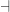 , not
, not 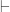 .
.
It seems appropriate to me to mention in Appendix A that this reformulation is only possible in a sufficiently strong metatheory; for instance it is not possible in Coq.
Your comments are much appreciated, thanks!
Actually, I found the stuff about adjunctions a bit boring… The only thing that I did there was replace equality by paths (or homotopies) and replace bijections by equivalences and then I had to see if the categorical argument would still go through. So from that perspective, there’s not really much in it. To be honest, I don’t really know much about homotopy coherence except that it exists and that it’s a delicate issue. But do you think that in this case the homotopy coherence is taken care of by the equivalences, i.e. by the contractibility of the hfibers? Contractibility seems to be good at such things. For instance when comparing two notions of injectivity

 ,
,
the one using contractibility seems to be preferable since it will also take care of injectivity at the level of paths (and higher up).
E.g. the map from the circle to unit should not be injective, but it would be according to the first notion.The second notion is like the first + coherence, if I’m not mistaken.I will soon upload a repaired version of the thesis. Thank you again for the comments!
Edit: It looks like the remark about the circle was false.
Well, equivalences do take care of a fair amount of homotopy coherence. However, your “functors” are not homotopy coherent (they preserve composition and identities up to a path, but that path has no higher paths attached to it), and similarly the adjunction equivalences are not coherently natural.
Hi!
So I read your master’s thesis last week. I’ve been following the blog stealthily for awhile so I was somewhat familiar with the ideas, but I enjoyed reading through a single document that explained things quite well. Nice job!
What I wanted to ask you & the rest of the group about is what work is being done on a more general mechanism for higher inductive types? I’ve read Awodey et al.’s paper on W-types in HTT, but those aren’t higher inductive types.
As far as I know there is not yet a general formulation that nails down what the higher inductive types are. But I would not dare to say that W-types could not be higher inductive types. They are not intended as such, but it seems likely to me that a theory with both W-types and all the spheres has a lot of spaces with interesting higher structure. There are maybe others who know more about the situation W-types + spheres.
Higher inductive types include ordinary inductive types, as the degenerate case where there are no path-constructors, only point-constructors. Since W-types are in turn a particular case of ordinary inductive types, they are also a particular case of higher inductive types.
Peter Lumsdaine and I are writing a paper about higher inductive types which will give a precise formulation of them, in some generality at least (perhaps not maximally), and construct them in homotopical models of type theory. My current hope is that it will be done before the end of 2012.
That would be most welcome!
Steve
I think I may have found a small typo in section 2.5.1 (A weak version of the axiom of choice).
In the definition of Choice(R), R does not make an appearance. Instead, we have an ill-typed P.
choice(R) := Sigma (s : Pi x:A. P x). Pi x:A. P(x, s(x))
should be
choice(R) := Sigma (s : Pi x:A. P x). Pi x:A. R(x, s(x))
Anyway, thank you for writing your thesis. HoTT is very fascinating, and your paper is the best chance a programmer like me has at understanding any of it 🙂