I recorded our local Seminar on foundations in which I talked about the notion of equivalence in HoTT:
Hopefully some people will find some use for it. It is pretty slowly going, and it might motivate some of the strange things going on in Equivalences.v.
It’s surprisingly hard to prove that is_equiv and is_adjoint_equiv are equivalent! I end up fooling around with lots of transport along funexts and needing new lemmas about transporting in iterated total spaces, and I’ve never been sufficiently motivated to make it work.
Well, I finally managed to prove this. I was going about it too directly — turns out it’s easier to massage them both step-by-step through a series of basic equivalences until they come out the same. See this file.
I also finally proved (same file) that the other possible definition, called is_hiso in Equivalences.v, is equivalent to is_equiv. That one is significantly easier. Of course, both proofs use function extensionality.
Excellent, thank you!
And they are equivalent, correct?
Well, since is_equiv is a prop and we have maps in both directions, their being equivalent is equivalent to is_adjoint_equiv being a prop. That doesn’t seem to be any easier to prove in Coq, but homotopical and higher-categorical intuition says that it’s true.
For instance, we could consider the theory of “marked simplicial sets” in section 3.1 of Higher Topos Theory, which are simplicial sets equipped with a subclass of “marked” 1-simplices denoting “equivalences” (thus a higher-categorical version of “categories with weak equivalences”). Any quasicategory has an underlying marked simplicial set
has an underlying marked simplicial set 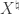 in which all the equivalences are marked, and any simplicial set
in which all the equivalences are marked, and any simplicial set  gives rise to a marked one
gives rise to a marked one 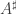 in which all edges are marked.
in which all edges are marked.
Let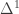 denote the 1-simplex, and let
denote the 1-simplex, and let  denote a simplicial set such that maps
denote a simplicial set such that maps  consist exactly of the data corresponding to is_adjoint_equiv. Thus
consist exactly of the data corresponding to is_adjoint_equiv. Thus  has two 0-simplices
has two 0-simplices  and
and  , two 1-simplices
, two 1-simplices  and
and  , 2-simplices
, 2-simplices  and
and 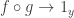 , and one 3-simplex exhibiting one triangle identity between
, and one 3-simplex exhibiting one triangle identity between  and
and  . Then the induced inclusion
. Then the induced inclusion  is “marked anodyne” (
is “marked anodyne” ( can be obtained from
can be obtained from 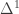 by gluing on two horns). Since the fibrant marked simplicial sets are just the objects
by gluing on two horns). Since the fibrant marked simplicial sets are just the objects 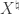 for
for  a quasicategory, this implies that the induced map of simplicial sets
a quasicategory, this implies that the induced map of simplicial sets  is a trivial fibration. Hence, any equivalence in a quasicategory
is a trivial fibration. Hence, any equivalence in a quasicategory  has a contractible space of extensions to adjoint equivalence data (the corresponding fiber of this map).
has a contractible space of extensions to adjoint equivalence data (the corresponding fiber of this map).