This post is to alert the members of the HoTT community to some exciting recent developments over at the n-Category Cafe.
First, some background. Some of us (perhaps many) believe that HoTT should eventually be able to function as the internal language of an -topos, in the same way that extensional type theory provides an internal language for ordinary topos theory. The basic structure is already there: any
-topos can be presented by a model category, whose (acyclic cofibration, fibration) factorization system should model identity types. Peter Lumsdaine and I are working on modeling higher inductive types in such a model category; univalence is a thorny problem.
However, we don’t have to wait for the details of this interpretation to be nailed down to start using it. We can start using HoTT “internally” to a class of -toposes by adding axioms that represent properties or structure possessed by such toposes, akin to how we can do synthetic differential geometry or synthetic domain theory “synthetically” without having a particular topos in mind as a model.
I have thought for a while that Urs Schrieber’s notion of cohesive -topos would be a good candidate for such development. The notion of cohesive 1-topos (or, more generally, cohesive category over a base) is due to Lawvere: it is a connected, locally connected, local topos E satisfying some additional axioms. This essentially means that in its global-sections geometric morphism to Set, the inverse image functor (called Disc) admits a further left adjoint (called
), and the direct image functor (called
) a further right adjoint (called Codisc), and moreover Disc and (equivalently) Codisc are fully faithful.
The intuition is that the objects of E are “spaces” — sets equipped with some “cohesion”, such as a topology, a smooth structure, etc. The functor gives the underlying set of points of a space; Disc equips a set with “discrete cohesion”; Codisc equips it with “codiscrete cohesion”; and
computes the set of connected components of a space.
A cohesive -topos is similar, but in the world of
-categories: it is an
-topos whose global-sections geometric morphism to
–Gpd (the
-topos corresponding to Set) is part of a 4-term adjoint string, where the inverse image functor Disc is fully faithful (as is the other functor in the same direction, Codisc). Now the leftmost adjoint is
(or just
), the fundamental
-groupoid of a “space”.
Now, while all of this structure as stated talks about the relationship of one -topos to another, a useful fragment of it can be phrased purely insude the
-topos E, and thereby also inside homotopy type theory (regarded as the internal language of such an E). The fully faithful functors Disc and Codisc can be regarded as equipping E with full subcategories of objects called “discrete” and “codiscrete”, respectively, and the existence of the various adjoints means that the discrete objects are both reflective and coreflective, while the codiscrete objects are reflective. There is a further compatibility condition which ensures that the category of discrete objects is canonically equivalent to the category of codiscrete ones, and that the two “global sections” functors agree modulo this equivalence.
Note that nothing in these axioms, phrased elementarily in terms of E, asserts that the category of discrete objects “is” –Gpd. Of course, that fact is not visible to the internal logic of E. Similar sorts of “internalization of the base topos” has also been used in ordinary topos theory, for instance in Awodey and Kishida’s interpretation of first-order modal logic in a topos of sheaves. (This suggests that perhaps “cohesion” can be regarded as a sort of “modality”.)
Anyway, the point is: a recent discussion at the n-Cafe, leading up to the formulation of these axioms in HoTT, can be found in the comments to this post. Since Urs has found that a good deal of formal differential geometry can be developed inside a cohesive -topos (perhaps augmented with some additional axioms, akin to SDG), this raises the possibility of formalizing all of that inside HoTT and Coq/Agda. I believe Urs is now pushing ahead with such a project.
Thanks for this post, Mike!
One comment: remarkable about the axioms for cohesive $(\infty,1)$-toposes is not just, I think, that they naturally imply a good deal of formal differential geometry, but that moreover — and maybe primarily — they imply a good deal of formal differential _cohomology_ . (This is the reason for the title of my writeup.) Especially in the more general “unstable” version that one finds in an $(\infty,1)$-topos, this goes quite a long way, incorporating higher Chern-Weil theory and all which comes with that.
Since to some extent one may think of higher Chern-Weil theory as being all about “higher gauge theory” I liked to think of general $(\infty,1)$-toposes as encodeing “kinematics” (cohomology) and of cohesive $(\infty,1)$-toposes as adding “dynamics” to this.
What I would now like to understand, given your comments above, is how that might be related to modal logic. Could you maybe expand on what you have in mind here?
This is done for local maps of 1-toposes in the following paper: “phrased elementarily in terms of
“phrased elementarily in terms of  ” — as Mike says — and then use it to determine the modal logic in
” — as Mike says — and then use it to determine the modal logic in  resulting from the local map.
resulting from the local map.
Elementary axioms for local maps of toposes. S. Awodey and L. Birkedal, Journal of Pure and Applied Algebra, 177 (2003), pp. 215-230.
There we give an axiomatic description of a local map
Some philosophers have looked into the modal content of classical mechanics. In particular, Jeremy Butterfield in here and here:
Of course, Jeremy is alive to the role of topos theory in physics.
David writes: “Some philosophers have looked into the modal content of classical mechanics. In particular, Jeremy Butterfield in here and here:”
My impression was that Mike had something more concrete in mind, specifically concerning the axiomatics of cohesion and modal logic. It seems that I might first of all need to get hold of a good account of modal logic in the first place, preferably one that is naturally adapted towards the nature of the present discussion. Does anyone have any suggestions?
David writes: “Of course, Jeremy is alive to the role of topos theory in physics.”
One should however note that Butterfield and those who now follow his topos-theoretic ideas in physics, as developed with Isham, is looking at possible roles of topos theory in physics that are quite different from the role of cohesive toposes. Or to put it differently: Lawvere has been advocating a role of topos theory in physics all along, and this is different (disjoint) from what Isham-Butterfield have suggested to look at. Cohesive topos theory is about the geometric aspects of physics.
P.S. Where can I find out which formatting commands this blog understands? What’s the right coding of blockquotes, of inline math and of italics/boldface?
Urs, you can use any sort of LaTeX; you just have to put the five characters “latex” immediately after the opening dollar-sign. (Yes, that’s sure intuitive… I have no idea why wordpress made it that way.) There’s a link to an explanatory page on the front page of the HoTT site. For formatting other than that, I believe you have to use HTML.
Steve, thanks for the link! I should have linked to that paper too; I did read it a while ago, and although it didn’t come to mind when I was writing this post, it probably it subconsciously influenced coming up with this axiomatization of cohesiveness. Unfortunately, we can’t do something exactly analogous to what you did there, since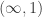 -toposes don’t have a notion of Lawvere-Tierney topology. They do have subobject classifiers, of course, but a left-exact-reflective subcategory (still the right notion of sheaf
-toposes don’t have a notion of Lawvere-Tierney topology. They do have subobject classifiers, of course, but a left-exact-reflective subcategory (still the right notion of sheaf 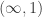 -subtopos) isn’t uniquely determined by the collection of monomorphisms it inverts.
-subtopos) isn’t uniquely determined by the collection of monomorphisms it inverts.
However, I think that paper is exactly the sort of “modal logic” that I was thinking of. Here’s the idea:
Sadly, the modal system defined at the end of Awodey-Birkedal uses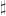 for interior and
for interior and 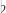 for closure, which is the opposite of how we’re using them. But they observe that the interior operator behaves like the necessity operator
for closure, which is the opposite of how we’re using them. But they observe that the interior operator behaves like the necessity operator  in modal S4.
in modal S4.
I don’t recall why we chose this unfortunate convention for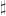 and
and 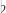 — maybe because of the connotation of “sharpening up” and “flattening out” an object, as opposed to the musical ordering.
— maybe because of the connotation of “sharpening up” and “flattening out” an object, as opposed to the musical ordering.
Thanks for these comments about modal logic, Mike. Now I am getting the idea.
Let’s maybe think a moment about the actual geometric interpretation of these “modalities” in the context of cohesion. There might be a very natural story to be told here.
Consider the following example: let the cohesive topos be that of smooth cohesion (sheaves over the category of smooth manifolds) and consider in there the proposition “the -form
-form  is closed”, presented by the monomorphism
is closed”, presented by the monomorphism
 .
.
This is not generally true. But it is true over every discrete space (somewhat trivially, but still). And formally we find that this fact corresponds to the fact that is an isomorphism (because already
is an isomorphism (because already 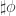 is).
is).
Therefore maybe what you suggested to read as “is codiscretely true” should actually be called “is discretely true” and geometrically means: is true over every discrete space. .)
.)
(The fact that discrete and codiscrete interact here is of course the fact that they share the functor
I have started to make some tentative notes along these lines at cohesiver topos — Internal modal logic.
But let’s think more and about more examples to better fine tune the interpretation further.
Darn. A bunch of syntax typos. There is neither a way to preview nor to edit a comment on this blog here, or is there?
Not for you, I don’t think. It is much inferior to the Cafe. But I, with fancy administrator powers, can edit your comment and fix the typos. (-:
I have posted a second installment about ongoing work on using axiomatic cohesion to obtain encodings of structures in differential cohomology theory in terms of homotopy type theory. See
http://golem.ph.utexas.edu/category/2011/11/hott_cohesion_exercise_ii.html
One point that these “exercises” are meaning to make manifest is that cohesive higher topos theory/homotopy type theory provides a way to speak about differential cohomological notions that is uncomparably shorter, hence more illuminating, than what one would get from formalizing the standard textbook axiomatizations of these structures — if one would succeed with that at all. Just imagine what it would take to have a something like a [ForMath project](http://wiki.portal.chalmers.se/cse/pmwiki.php/ForMath/ResearchMethodology) to encode in Coq the notions and properties of smooth manifold, tangent bundle, cotangent bundle, differential forms, de Rham hypercohomology and then finally Deligne hypercohomology.
But in cohesive HoTT, we get there, I claim, in just a few fairly elementary steps.
Where of course part of the trick is to skip over the explicit definition of a manifold and instead find intrinsic homotopy-theoretic characterizations of the various differential objects. In section 3.3 of my writeup it is shown that when these abstract structures are realized in a suitable model, then they do reproduce the standard constructions from the traditional textbooks.
A further note: after additional discussion, we realized the axioms we started with were too naive to be correct in the models. A discussion of a (hopefully) corrected set of axioms, with links to Coq code, can be found here. I think the role of “higher modality” is even clearer now.