4 Responses to Another Formal Proof that the Higher Homotopy Groups are Abelian

1. Mike Shulman says:

   13 April 2011 at 18:34

   Nice! It looks simpler than I expected. I’m intrigued by your comment in the source that proving adjust_l (and, I presume, adjust_r) by induction didn’t give a term that was explicit enough. I’ve had a similar experience with the induction proofs of equiv_inv, equiv_inv_is_section, and equiv_inv_is_retraction, but I thought that maybe I was doing something wrong. It’s too bad if the convenient induction tactic has a tendency to produce proofs that aren’t good enough for further use. Are the proofs “really” different, or is Coq just not able to figure out that they’re the same?

   I also have to repeat my suggestion that we say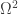 rather than 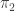when that’s what we really mean. (-:

   Reply
2. Jeremy Avigad says:

   15 April 2011 at 17:03

   Thanks, Mike.

   In fact, I was just able to prove the two proofs (i.e. paths) are homotopic to one another; see the code below.

   What’s going on is that when it comes to Omega^2, the two endpoints of a path p are the same; so induction over p no longer works, and it become impossible to simplify j terms over paths. So one needs a description of the homotopy that doesn’t require unpacking a j-term.

   The fact that “proofs” are far from irrelevant here — e.g. they can describe paths that one wants to reason about — makes me uneasy. The particularities of a proof can have an effect on future developments in ways that I still don’t fully understand. For example, Dan pointed out to me that his code only needs one “adjustment” (whereas I need adjust_l and adjust_r) because he used a different definition of concatenation/transitivity than Andrej did. Roughly, Andrej (proved transitivity “trans p q”) / (defined concatenation “p @ q”) by contracting both p and q, which has the effect that “id_path x @ idpath_x” is definitionally equal to “idpath x”. But if you prove it instead by contracting only the first, say, then you get the more useful property that “id_path x @ p” is definitionally equal to “p”. That better definition would have made my code a bit shorter.

   Welcome to the wonderful world of proof relevance.

   *****

   Lemma adjust_l {A} {x y : A} {p q : x ~~> y} (R : p ~~> q) :
   idpath x @ p ~~> idpath x @ q.
   Proof. exact (idpath_left_unit p @ R @ !(idpath_left_unit q)). Defined.
   (* induction R doesn’t given a term that is explicit enough. *)

   Lemma adjust_l2 {A} {x y : A} {p q : x ~~> y} (R : p ~~> q) :
   idpath x @ p ~~> idpath x @ q.
   Proof. induction R. apply idpath. Defined.

   Lemma test {A} {x y : A} {p q : x ~~> y} (R : p ~~> q) :
   adjust_l R ~~> adjust_l2 R.
   Proof.
   induction R; induction x0.
   path_via (idpath_left_unit (idpath x) @ idpath (idpath x)).
   Qed.

   Reply
   • Mike Shulman says:

     18 April 2011 at 15:01

     Fascinating! It doesn’t really bother me too much that these “proofs” are “relevant”, because as a homotopy theorist, I don’t call these things “proofs of theorems” but rather “constructions of paths.” And “obviously” when you construct a path, it can matter which path you construct. (-: But it does seem a little unfortunate that we have to pay attention to details like this.

     Reply
   • Peter LeFanu Lumsdaine says:

     18 April 2011 at 21:00

     It seems to me that the basic status of proof-irrelevance — the idea that certain types are in some sense “propositions”, and for them one should have proof-irrelevance — hasn’t changed; we’ve simply jettisoned the principle that equality should always be such a proposition.

     Indeed, arguably we haven’t even lost that much! It’s quite consistent that there’s a “π_{-1}” construction, reflecting types into homotopy-propositions, which are (at least propositionally) proof-irrelevant; and then this applied to the identity type gives a homotopy-proposition representing equality — so, a proof-irrelevant equality. What this lacks compared to full identity types is that one can only eliminate out of it into other homotopy-propositions, not into arbitrary types.

     Reply